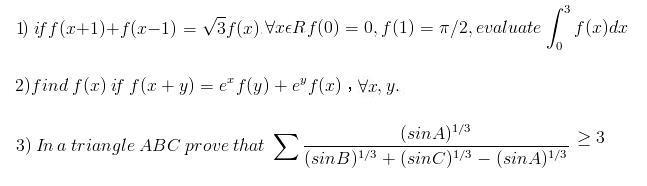Q2) Divide throughout by e^{x+y} to get
\dfrac{f(x+y)}{e^{x+y}}=\dfrac{f(x)}{e^{x}}+\dfrac{f(y)}{e^y}
Set g(x)=\dfrac{f(x)}{e^{x}} and the given equation becomes
g(x+y)=g(x)+g(y)
which is the Cauchy's equation having solutions
g(x)=kx
Hence,
f(x)=kxe^x
5 Answers
3rd one can be settled with ease.
Ur inequality is same as proving \sum{\frac{\sqrt[3]{a}}{\sqrt[3]{b}+\sqrt[3]{c}-\sqrt[3]{a}}}\ge 3
Let's see this...assuming (a,b,c) to be the sides of a triangle, we can prove that (\sqrt[3]{a},\sqrt[3]{b},\sqrt[3]{c}) are also sides of a triangle.
My proof for this is very unelegant - basically what I did was to have a+b+3\sqrt[3]{ab}\left(a^{\frac{1}{3}}+b^{\frac{1}{3}} \right)>a+b>c\Rightarrow a^{\frac{1}{3}}+b^{\frac{1}{3}}>c^{\frac{1}{3}}. & .....
So now make the substitution a=x^3, b=y^3, c=z^3
From which we simply have the inequality reduced to proving \sum{\frac{x}{y+z-x}}\ge 3
Which follows from A.M-G.M on the terms and using the fact
\prod{(x+y-z)}\le xyz.... Done.
Similar to Soumik's. The proof of the inequality is different, maybe longer