THE NUMBER OF OUTCOMES POSSIBLE OS 4 IN YOUR EX . OUT F WHICH 2 ARE FAVOURABLE . HH AND TH ? SO PROBABLILTIT IS 1/2 . RIGHT?
From a pack of cards two cards are taken out and thrown away. Now a card is drawn at random.Find the probability of the card to be an ace.
-
UP 0 DOWN 0 0 27

27 Answers
If you define
E as Probability of Picking an Ace on 3rd card.
E1 as the probability of picking an Ace on 3rd card.. given no Ace was picked on the first two cards... and so on...
Then what u are saying is correct :)
yes
but if u take it as the sum of two subcases i made it would have become 1! isnt it?
yes there is ... but i think it is equally or more important to understand the theorem and not to learn...
see my example u will understand partly what is happening!
THEN p(E/S) = p(E/E1) + p(E/E2) + p(E/E3) + p(E/E4)
NO!
This is not true...
Actually
THEN p(E/S) = p(E/E1).P(e1/E) + p(E/E2)P(E2/E) + p(E/E3)P(E3/E) + p(E/E4) P(E4/E)
the circle is the event taking place . i.e. E .
then we have to find the probability of E wr.rt to each case.
AS WE DON'T KNOW WHICH OF THE FOUR EVENTS HAS MORE CHANCES. E1 ,E2 ,E3E, E4 I MEAN WE ASSIGN EQUAL PROBABLITIES IRHGT? , THEN p(E/S) = p(E/E1) + p(E/E2) + p(E/E3) + p(E/E4)
I think so.
why don't they add up?
I will give u an example.
E = What is the probability that u get a head on second toss.
If you get E1= 1st toss is head
E2= 2nd toss is head
Probability of head on 2nd toss is 1/2 in both cases...
if u add probability it will become 1/2 + 1/2 which is 1!!
which is clearly wrong..
This is what i am trying to confirm from you!
wiat amin then , it's only yesterday we started it. I think I might be wrong in my statemetn . one mo .
yes the cases are correct..
But the probability will not be the sum of probabilities!
Tell me what probability are u fining.. in each case... "Exactly what"
Then i can tell u if what u are thinking is correct or not!
Arjita and mine are same , except that I've wriiten it in a daig.
E1 - when you drwaw a card from teh pack of 50 with , 1 ace and 49 - others and so on. A- ace , O-thers
sorry dude i did not understand clearly what u mean by the four parts!
I mean u have to define to me E ,E i etc... sorry buddy...
I get a feeling of what u r trying to say by this picture... but the whole thing is not clear to me :(
I didn't get the 3rd card Ace argument. I'm tellin w.r.t Abhirup's Q , even though U say , It's the same . I'll try to understna , I fnot I'll clarify my doubt from you . is my ststement w.r.t Abhirup's Q right?
Well ... as nothing is told about the two cars that have been taken out .. I think the probability wont change [1]
Just a guess ...
let S be the sample space. and E be the event.
then the probability of E takning place is p(E/S) S NOW CONTAINS 50 CARDS. SO ,cases possible are , E1 , E2 ,E3 ,E4 as indicate din the diag.
so ,now probability becomes , p(E/S) is the intersection of all possibilities.
i.e. it adds up . Right?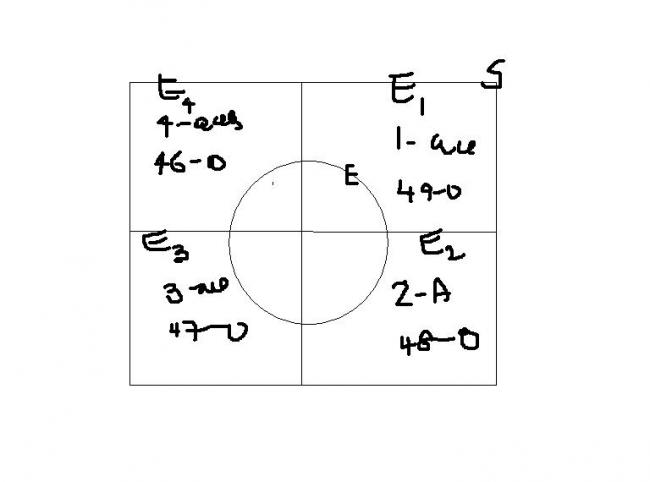
ok i got it but is the traditional approach for such problems which i got (just 4 checking my basic theorems on probability) correct:
req prob=
(48C2/52C2)*(4C1/50C1)+(4C148C1/52C2)*(3C1/50C1)+(4C248C0/52C2)*(2C1/50C1)
Ok .. try to think of the case where 51 cards are thrown away in place of 2.
Then what will be probability of getting an ace after throwing 51 cards ?
As there will be only one card left, so its something like you draw 1 card & throw rest of them[3] ... and the probability of drawing one ace is 4/52
So you can see that whether you draw one card in begining or after throwing 51 cards randomly ... the probability remains the same 4/52 [1]
See the probablility of the nth card being an ace is the same no matter whether n is 1 or 2 or 3 or .... 52... (As long as we do not know any of the other cards!)
It is 4/52.
The "3rd" card here comes because we have taken the other two cards out of the pack. So the 3rd card ...
Answer will be 4/52
Arjita is right the method we follow will be the same as he is trying..
There could be another much simpler way to think
The cards are arranged in order. What is the probability that the 3rd card is an ACE!
This is clearly 4/52!
@arjita
I didn't get the case 3 & case 4
Look there can be ony 3 cases, among the 2 cards thrown :-
1: 1 ace & 1 other card is present
2: 2 aces are present
3: No ace is present
p(1) = 4C1 x 48C1 / 52C2
p(2) = 4C2 / 52C2
p(3) = 48C2 / 52C2
can their be four cases....
1) that 2 cards are thrown from 48 cards n 4 aces are safe and then we will select i ace from that 4 ace...
2) 2 cards are thrown from 49 cards n then ace is selected from remaining 3
3) 50 cards n 2 ace
4) 51 cards and 1 ace
But nothing have been told abt the thrown cards !!
So I think that the even if one calculate taking into account the probability of ace being thrown away .. the result will be same.
Well its just my intutions & some concept of probability.
I am not sure abt it :) ... let the forum Experts think about it.
i don't think that way what if one or may be both ace are thrown away...
So according to you the probability of getting an ace
= initial no of aces in pack/total no of cards
= 4/52 = 1/13
Is this you are trying to say ? [7]