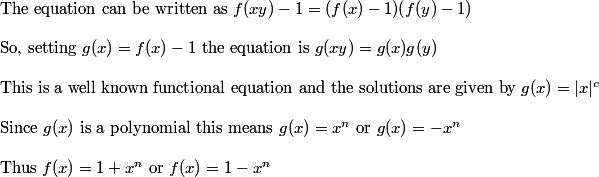2305Let
f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{0}
f\left(\frac{1}{x}\right)=\frac{a_{n}}{x^{n}}+\cdots +a_{0}
f(x)\cdot f\left(\frac{1}{x}\right)=a_{n}a_{0}x^{n}+(a_{n-1}a_{0}+a_{n}a_{1})x^{n-1}+\\.\qquad \qquad\qquad\cdots +(a_{n}^{2}+a_{n-1}^{2}+a_{n-2}^{2}+\cdots +a_{0}^{2})+\cdots +\frac{a_{n}a_{0}}{x^{n}}
a_{n}a_{0}=a_{n}\rightarrow a_{0}=1
After comparing the terms we will find that an=±1 and a0=1.All the other terms are 0.
f(x)=1+x^{n}\text{ or } 1-x^{n}
2305
Shaswata Roy
·2013-08-21 03:27:28
We can also consider the function h(x)=f(x)-1
Then,
h(x)*h(1/x)=1
Now it's easy to see that h(x)=±xn
1Can you guys prove this why the function is polynomial function.Because I also did the way which shaswata did. But i cannot make out why the solution of this function is only a polynomial function.
341The question sought a polynomial to begin with.
In general, h(x) for x ε R-{0} (as in Shashwata's reply) can be constructed in infinitely many ways. One example would be h(x) satisfying:
(1) h(1) = 1
(2) h(x) = t ; x ε (0,1)
(3) h(x) = 1/t x>1
(4) h(-x)=h(x)
for any non-zero t
Then f(x) =1+h(x)
man111 singh Nice solution shaswata RoyUpvote·0· Reply ·2013-08-20 03:51:23
