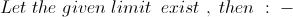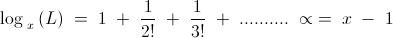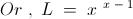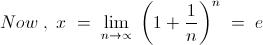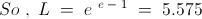30
30Btw, I'm not your BHAIYA bhaiya! [3] lol. I'm have just come to class 12. :)
I don't know aren't all terms multiplied?
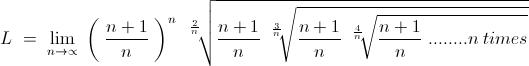
so like the first term under root is the 2/nth root of (n+1)/n which is further multiplied to 3/nth root of (n+1)/n which already under the 2/nth root.
Essentially what I mean is that isn't it,
L = \lim_{n\rightarrow\propto }\left( \frac{n+1}{n}\right)^n \left(\frac{n+1}{n} \right)^{\frac{1}{2/n}} \left(\frac{n+1}{n} \right)^{(\frac{1}{2/n})(\frac{1}{3/n})} .....
 1
1ricky..
check that u'll get
LOG{x} L= e-1........not x-1[think why!!]
though ans will remain same...e^(e-1)..coincidentaly:)
 1
1me too didnt get the step where ricky bhaiya took log
please explain
 1
1ricky i did not get what u did in the step where u took log of the series...cn u plz elaborate!
 71
71Yes.. now got it.. That was the only culprit (worm) that infected both of us - Nishant Sir and me :P
Ab toh abda aasan hai ! :P :P
If you more collection for good problem that I should try then please let me know. You may post them in my Chatbox. Plz
 1
1No , if you look more closely . See , the " n - th " root of " x " = x 1 / n
Hence , suppose if you want the " 2n - th " root of " x " , that should be = x n / 2 .
 62
62agree to vivek.. cos that is something that i also tried as soon as i saw the question...
I mean substituting it by x... b;ut that din help at all!
 71
71Ricky bhaiya, I have a serious doubt in your solution STEP 2# where you take
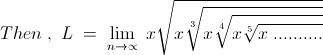 , .................. (i)
, .................. (i)
You have assumed 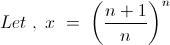 ,
,
BUT In RHS of 1you are taking Index of root of x as 2,3,4 ....
Won't that be kind of xn3 , xn4 , Instead of what you have posted in the problem where Indexes of root are x3n, x4n ..
Correct me as It may be a serious problem for me.
 1
1You don't sound foolish at all : )
Here goes my solution then : -
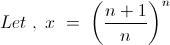
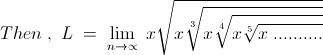
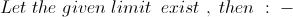
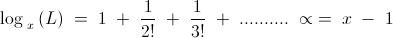
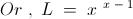
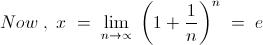
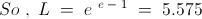
 30
30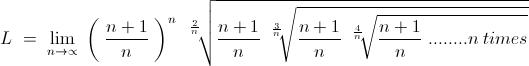
= \lim_{n\rightarrow \propto }(\frac{n+1}{n})^{\sum{\frac{n^k}{k!}}}
= \lim_{n\rightarrow \propto } (1+\frac{1}{n})^{e^n-1}
= \lim_{n\rightarrow \propto } ((1+\frac{1}{n})^n)^\frac{e^n-1}{n}
= \lim_{n\rightarrow \propto } ((1+\frac{1}{n})^n) \lim_{n\rightarrow \propto } \frac{e^n -1}{n}
= ∞ [7]
 1
1Sorry , that does equal the given expression . But still , it possesses some finite value .
 30
30But isnt it,
L=\lim_{n\rightarrow\propto }\left( \frac{n+1}{n}\right)^n \left(\frac{n+1}{n}\right)^{n/2}\left( \frac{n+1}{n} \right)^{n^2/6} ...
 71
71May be I took it took the hint seriously :P Aur try karta hoo
 71
71Ricky Bhaiya, is any of these one answer to your sum :
e or 1
I have just tried to see. Let me know plz
 62
62yaar kuch dikh to nahi raha :D
bata de kya gadbad hai :P
 1
1Nishant sir and Ashish Bhai , are you sure what you have written are correct ? Please check once more on my behalf .
 62
62srry it will be e to pwer infinity...
 30
30okay..got the mistake sir.. Thanks! :)
 62
62ashish.. the actual sum is
\left(\frac{n+1}{n} \right)^{n+n/2+n^2/3!+n^3/4!...} \\=\left(1+\frac{1}{n} \right)^{3n/2+n^2/3!+n^3/4!...} \\=\left(1+\frac{1}{n} \right)^{n(3/2+n/3!+n^2/4!...)} \\=\left(\left(1+\frac{1}{n} \right)^n\right)^{(3/2+n/3!+n^2/4!...)}
=e3/2
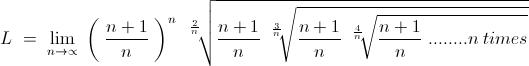
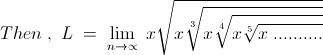 , .................. (i)
, .................. (i)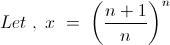 ,
,