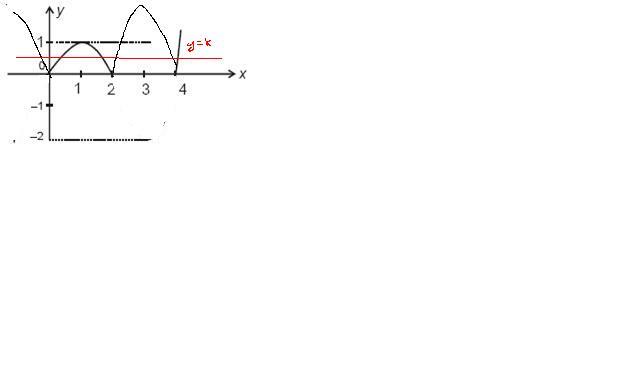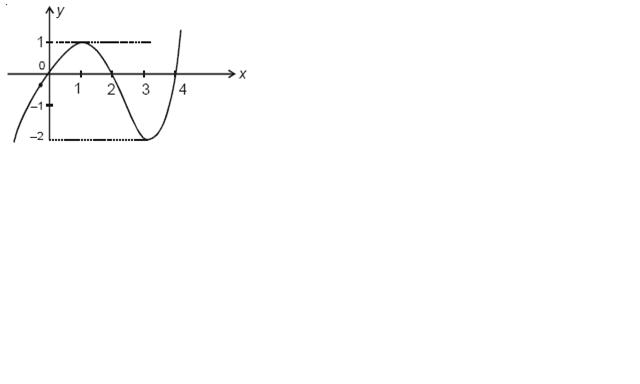4Yeah u're right !
But plzz post the solution
Again some maths questions:
Q1. (Multi-Answer)
Domain of the function
f(x) = log_{[x-1]}(sin^2\pi x) \; is \;x\epsilon (3,\infty )-\begin{Bmatrix} p, & p+1, & p+2, & ..., & n \end{Bmatrix}, where [.] denotes greatest integer function and n is a multiple of 4 and 25, then
(p) + (p+1) + (p+2) + ... + n can be
(a) 5047 (b) 20097 (c) 5050 (d) 45147
Q2. (single answer) The number of regions into which a set of lines divide a plane is n and the maximum number of points of intersection of these lines is m. If the number of lines in the set is \frac{n+m+P}{n-m+P} then the possible value of P is
(a) 0 (b) -2 (c) -1 (d) 4
-
UP 0 DOWN 0 1 21
21 Answers
106Its wrong because:
see #17.
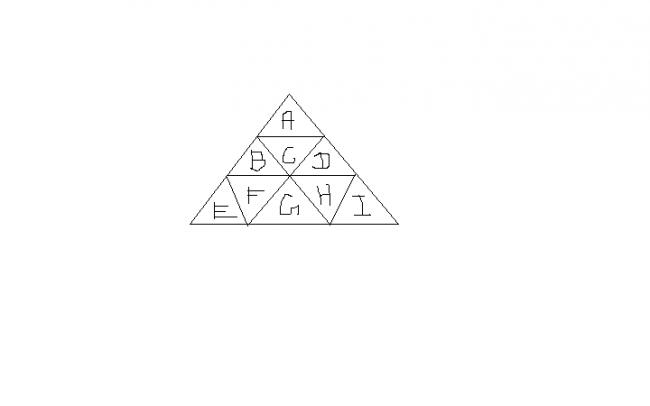
A can have 9 colours so C will have 8.
=> B,D can have 8 each
=> F,H will also have 8 each
=> E,I will have 8 each
Now G can be filled in 7 ways (iff the colours of F and H are different)
If F and H have same colours then G can be filled in 8 ways.
So there will be two cases...
1plz upload the paper.
I am going to upload my aakash success magnet paper here . you also plz do them for all fiitjee brilliant or aakash
106@uttara: i wanted a method for that ... i got the answer by substituting the value like u have done but i wanted a method for that
1filling d triangles from any direction...let from top,triangle A can be filled by 9 colurs
triangle C with 8 colour( coz it cannot be filled with d colur dat A has),
triangle B and D also by 8 colours each,..so filling all
we get 9*8^8
4SECTION-III
Linked Comprehension Type
The graph of y = f(x) is given as following.
On the basis of this graph give the answers of the following questions
Ques. The interval in which k lies so that |f(x)| = k has maximum number of solutions, is
1. (0, 1]
2. (0, 1)
3. (1, 2)
4.[2,∞ )
I got the ans as (0,1] but given ans is (0,1) ??????
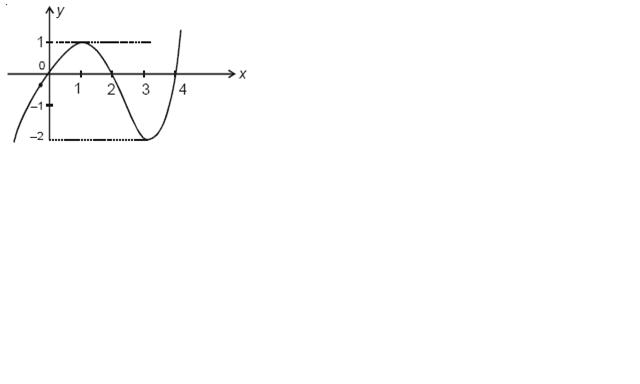
4This is also a qs from AIATS
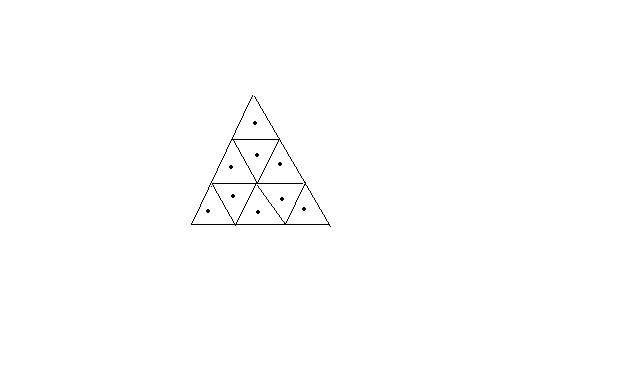
Q. 23 Number of ways in which we can colour the dotted triangles with 9 different colours available such that no two
consecutive triangles have same colours is
1. 9!
2. 8 × 98
3. 9 × 88
4. 99
