answer

sub P in terms of Q in the y=P+Q. find dy/dQ. u will get the value for Q.Sub these values in the d²y/dQ².the value which gives negative sign for the d²y/dQ² will be the maximum value.then use P+Q=1.

A graphical method can be much simpler.

take P and Q as the co-ordinate axis, then the constraint imlies that P and Q must lie on the circumference of a circle of radius 1.
Now, let P+Q=c

which in fact is a straight line having a P-intercept of c units.

It can be seen that c is maximum, with P and Q lying on the circle, happens only when the line P+Q=c touches the circle.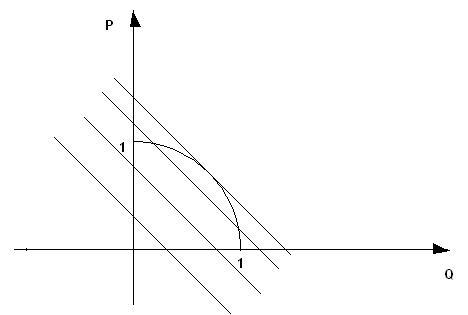

where P=Q (by symmetry)
or P=1/√2
and c=√2

P = sin a and Q = cos a

or Cauchy Schwarz gives 2(P²+Q²) ≥ (P+Q)²
gives P+Q ≤ √2