1Anant sir.... in the example given 011 is also invalid
number of valid binary words is coming to be (n+2)th term of fibonacci series
Define a "valid n-bit binary word" as a n digit long sequence of 0's or 1's in which no two or more consecutive 1's are present. For example, for n = 3, we see that of all the 3-bit binary words possible: 000, 001, 010, 011, 100, 101, 110, 111; exactly three ---- 011, 110 and 111 ---- are not valid but the rest of them are valid.
Question: Find out the number valid binary words formed with n bits.
P.S: Edited.
-
UP 0 DOWN 0 0 6
6 Answers
11for n=1 : 0 and 1 are two possible binary words
for n=2 onwards
suppose 1st digit is 0 then the nextr digit can be 0 or 1 (2 cases)
suppose 1st digit is 1 then next digit must be 0 (since two consecutive 1's can't occur)
so as n increases every 0 will produce 2 cases and every 1 will produce 1 case
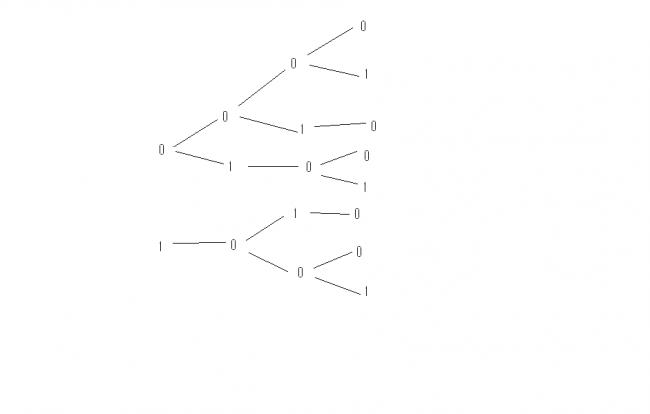
for n=1 : 2 cases
for n=2 : 3 cases
for n=3 : 5 cases
for n=4 : 8 cases
it is becoming a fibonacci series
\frac{(1+\sqrt{5} )^{n+2}-(1-\sqrt{5} )^{n+2}}{2^{n+2}\sqrt{5}}
66You won't call that a proof by looking at a few cases for n, will you? It must be proved for an arbitrary n.
341in other words, how can you prove that the recursion formula of fibonacci is applicable in this situation too?
1Actually it was kind of a hint or you may say half of the solution and i left for others to try and arrive till final step
by proceeding as shown in diagram above suppose for r digit 'xr' number of zeros are available and 'yr' no. of 1's are available (for r digits : no. of possible words , wr=xr+yr)
since each 0 provides with two cases next digit can be (0 and 1) and each 1 provides with 1 case (next digit is 0)
so, xr+1=xr+yr=wr and yr+1=xr
for r+1 : total no. words, wr+1 = xr+1 + yr+1
since xr+1 = wr and yr+1 = xr=wr-1
so, wr+1 = wr+wr-1
also we know w1=2, w2=3.....
the formula which I have shown can be derived by generating polynomials which i learned from Hari sir :)
http://www.goiit.com/posts/list/differential-calculus-hard-question-951552.htm