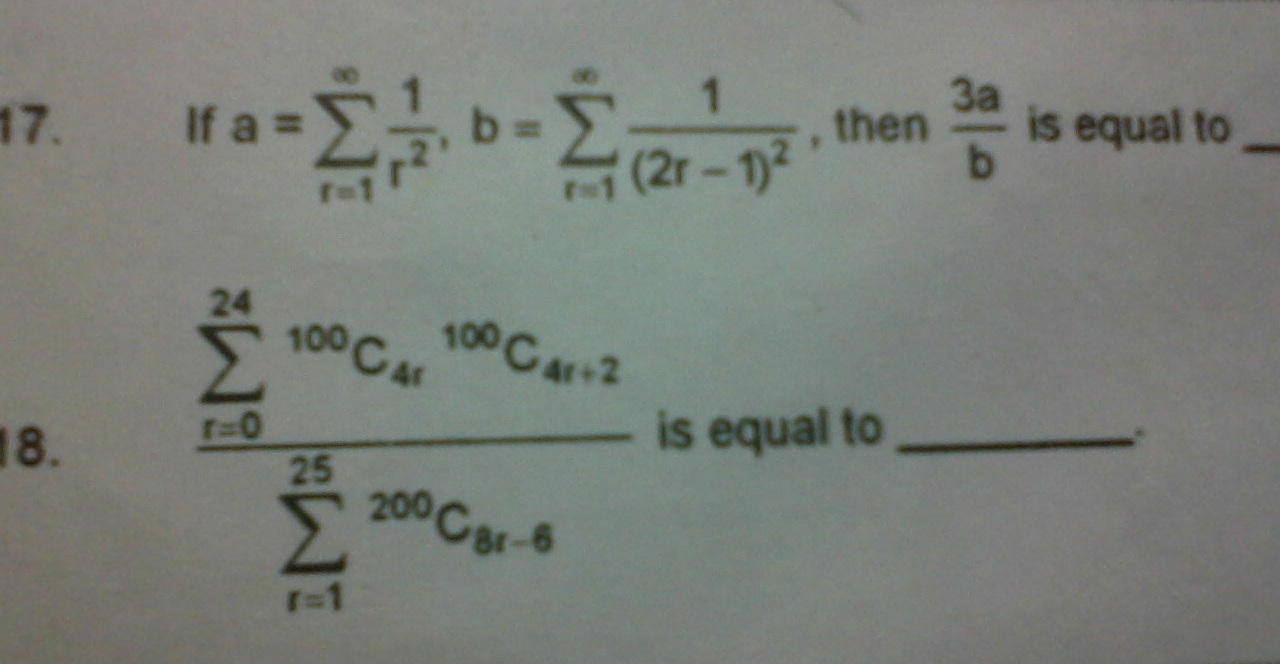BINO-numerical based

\hspace{-16}\bf{(1)\;\;} $Given $\bf{a=\sum_{r=1}^{\infty}\frac{1}{r^2}}\;\; $and $\;\; \bf{b=\sum_{r=1}^{\infty}\frac{1}{(2r-1)^2}}$.\\\\\\ Now from $\bf{a=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+.....\infty}$\\\\\\ $\bf{\Rightarrow a=\left\{\frac{1}{1^2}+\frac{1}{3^2}+\frac{1}{5^2}+\frac{1}{7^2}+.....\infty\right\}+\frac{1}{2^2}\cdot \left\{\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+.....\infty\right\}}$\\\\\\ So $\bf{a=b+\frac{1}{2^2}\cdot a\Leftrightarrow \frac{3}{4}a=b\Rightarrow \frac{3a}{b}=4}$