13Perfectly done Tushar...thnx [1]
If - Z= \frac{1}{^nC_0} + \frac{1}{^nC_1} +....+ \frac{1}{^nC_n}
Then, find the value of -
Z= \frac{1}{^nC_1} + \frac{2}{^nC_2} + \frac{3}{^nC_3}+....+ \frac{n}{^nC_n}
in terms of "n" and "Z".
-
UP 0 DOWN 0 0 2
2 Answers
11Z = 1 / nC0 + 1/ nC1 + ..........+ 1 / nCn
= 
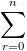1n C r
Now , Z ' = 1/ n C 1 + 2 / n C 2 + 3 / nC3 + ............+ n / n Cn
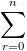= rn c r ................(i)
Now replace r by (n-r) in the eqn, we get
Z ' = 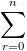(n-r)n C n-r
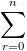= (n-r)n c r .............(ii) [bcoz n C r = n C n-r ]
Now adding eqn (i) and (ii), we get
2 Z ' = n 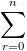1n c r = n Z (bcoz Z = 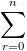1n c r)
Therefore, Z ' = (1/2) n Z