341Maybe this old thread in goiit will help: http://www.goiit.com/posts/list/algebra-progression-74421.htm
TOTAL 2 PROBLEMS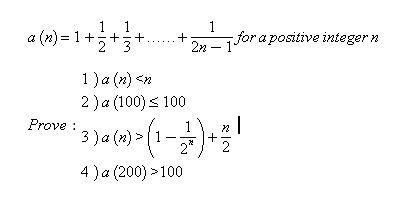
It Came in IITJEE 1999
How To Solve This One ?? PLease solve it in DETAIL Stating HOW you got this !
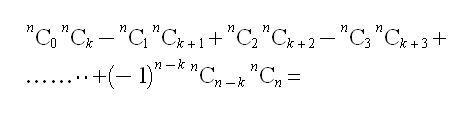
Answer in "nCr" or Factorial Form !!
-
UP 0 DOWN 0 2 6
6 Answers
1for q-2 is the answer
2nCn+k ???
\texttt{coefficient of }x^k \texttt{ in the expansion of } \\ \left( 1+\frac{1}{x}\right)^{n}\left(1-x \right)^{n}=\binom{2n}{n+k}
1nishant bhaiya , iron man is not having answer with him can u verify if my answer is right ?
62@Sonne... you are correct..
if we see the first question, we should observe that
a and b are straightforward adn there is nothing much to prove there..
If part c is true, then the 4th part follows directly by substituting n = 200
but first look i feel that the sum should be uptil 1/(2n-1) not 1/(2n-1)
341
6well
i practised problems from TMH for BINOMIAL THEOREM
and the problems were really tuff:(
i m having problem solving these problems!!!
