THIS ONE'S FRM DA TEST SECTION!!!
CAN SUM1 XPLAIN
Q1 Let the roots of f(x)=x be α and β where f(x) is a quadratic polynomial. It is true that α,β also satisfies f(f(x))=x. Let the other roots of the eqn. f(f(x))=x be γ and δ. Now Correct statements are:
a) If α β are real and distinct then γ and δ are not real.
b) If α+β=γ+δ then none of α β γ δ are real.
c) If α=β(real) then γ and δ are real.
d) None
Correct Answer: (b)
pl xplain
i have been thniking about this for the last 15 mins. !!
my God!
i am fed up !
not so easily sky!!!
others to pl. try yaar, this one seems to be an imp que. coz its based on a concept of quad... which is da key n ther is no boundary 4 qualty of que 2b asked!!!
cmon guyz!!!
confused yaar;
let f(x)=ax2+bx+c and ff(x)=a(ax2+bx+c)2+b(ax2+bx+c)+c
and also it is given dat the eqn ff(X)=x is satisfied by the roots α,β
therfore it implies dat a constant term is equal to a variable x ;dis is not possible; please help me were i went rong
arey kya easily?
this ate up my whole evening!!
mujhe chem padhna tha aaj !
poora giya :P :P
newaz, yeh bhi nahi bana :P
huh!
hindiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
pls translate
arre kya yaar sankara tujhe hindi nahi aati kya???
wat is our natnl lang????
SORRY SKY 4 SPOILIN UR EVE :(
can the maestros of math plz jump into this prob n pull us out of it!!!!
pl.....
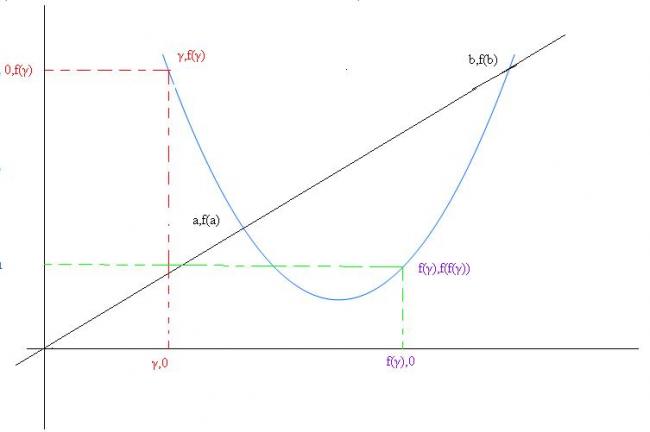
Consider any point γ,f(γ) on the curve...
Now consider point f(γ),f(f(γ)) on the curve...
as it is given γ is soln of f(f(x))=x...
there fore f(f(γ))=γ
there fore in fig below AB=γ
therefore red and green line intersects at y=x at (γ,γ)
or by geometry u can say point Q and B are miror images about y=x..
also δ also satisfies this
as if we would have taken A as (δ,0) then we would have got same things...
or in other words we can say that
point P and A are points (γ,0) and (δ,0)..
or u can say f(δ)=γ and f(γ)=δ.........(bcause f(f(x))=x has only 4 roots)
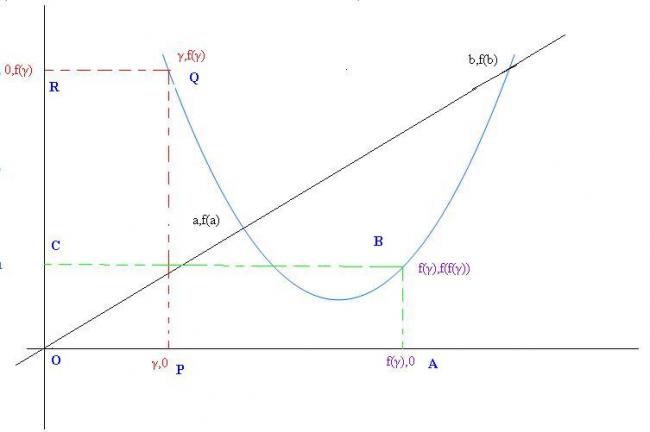
Now to check the options..
option a)
if real a,b exists then real γ,δ also exists... (in fig)
option c)
if a=b that means y=f(x) is tangent to y=x..
then no γ,δ exists as it is clear if one is above y=x other should be below y=x (mirror images)..
option b)
a+b=γ+δ
a+b=γ+δ...........(i)
2 2
also f(a)=a f(b)=b... f(γ)=δ and f(δ)=γ........(ii)
there fore from (i) and (ii) it follows that ..
f(a)+f(b) = f(γ)+f(δ)
2 2
or midpoints of (a,f(a)),(b,f(b)) and (γ,f(γ)),(δ,f(δ)) coincides or
(a,f(a)), (b,f(b)), (γ,f(γ)), (δ,f(δ)) forms parallelogram.. which is not possibles as all points are on parabola...
ABSOLUTELY AMAZING MAN!!!!!!11
THIS IS A MESMERIZING SOLN. INTERWOVEN WITH HARDCORE CONCEPTUAL MATHS!!!!!
GR8 WORK DUDE!!!!
CAN SUM1 PL. help me with a more time-SAvvy solution...........
and EVEN this technique is only PRIYAM's mastery, so v guyz gotta find another way out........
Pl. HELP. NEED A SHORTER METHOD IF ANY..........
THNX [1]