Bit of maths and physics

Well , how about some good questions to wake you up all night ? I think these are quite intriguing to attempt , so I will definitely post the solutions after a day or two ----

1> ( a , 1 / a ) , ( b , 1 / b ) , ( c , 1 / c ) , and ( d , 1 / d ) are the vertices of a cyclic quadrilateral . Find the relation between a , b , c , d . ( Trust me on this , this one’s got a fairly good solutions !!!!!! )

2> If a + b + c = the number of solutions of the eqn. e³ + e²f + ef² + f³ + 1 = 2002 , then prove that the eqn. ( n - 1 ) ax + ( n - 2 )bx + c = 0 has at least one root in the interval ( 0 , 1 ).

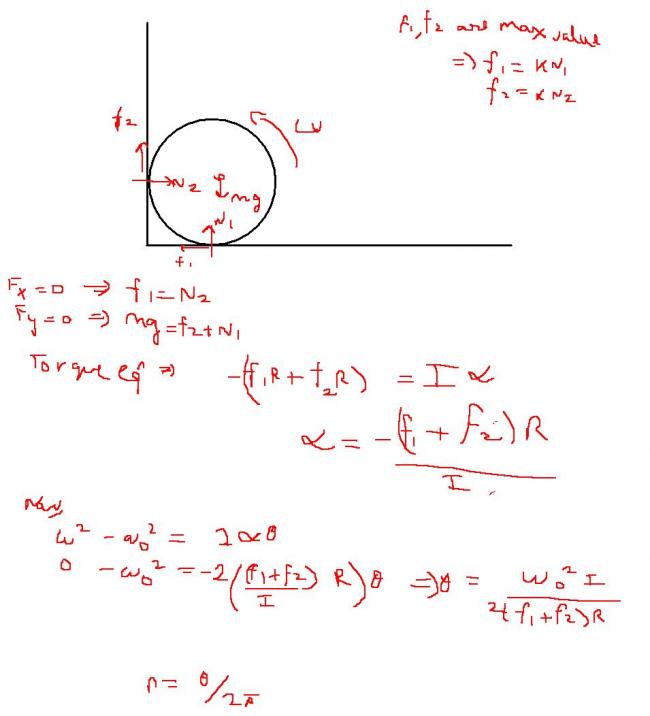
3> A uniform cylinder of radius R is spinned about its axis to the angular velocity W and then placed into a corner . The co-eff of friction between the corner walls and the cylinder is K . How many turns will the cylinder accomplish before it stops ?

4> A conical pendulum , a thin uniform rod of length L and mass M rotates uniformly about a vertical axis with angular velocity W ( the upper end of the rod is hinged ). Find the angle between the rod and the vertical.

5> Given that x , y , z are real , find them if x + y = 2 and xy = 1 + z² . ( very confusing , isn’t it ? But easy .)