1Maybe it wont.
Actually i myself didnt get the answer and had to see the solution.
This is a gud problem from Chinese olympiad.
How thick should a coin be to have a 1/3 chance of landing on edge?
-
UP 0 DOWN 0 2 58
58 Answers
1
62yeah may be that will give a hint... or u want me to post my solution before that?
i got somthing like
tan-1(t/2r) = 30
so t=2r/√3
3is this a question from mtg magazine
i thought that i wanted to post this thing :p.
i got the soln if u want the soln i will post
9feel 2r/√3 is right , ( even i m gettin same thing as nishant sir)
post ur sol aditya we ud like to see it
62Will my method work.. ?
when the center of mass of the coin lies with the base line (of the edge) it will not topple.... ?
SO it has to do with the angle .. so that the line throug the center of mass will lie withing the horizontal band
9how did u consider that
nishant sir and i ve considered angle by angle
62gaurav.. u have a very good method.. the only problem is that one area you have taken is not based on the surface area of the sphere...
I mean the area which u have taken in the numerator.. i think should be the area of the corresponding curved surface on the sphere...
But i think ur method does make a lot of sense...
There is a compeltely underlying difference in our approach..
i will try to explain that in the next post....
62see in my approach ... i am assuming that the coin is flipped and that the way it will fall will always be based on the flip...
in your approach, you are doing almost the same thing.. but i think ur approach allows the coin to be flipped in a different way than we do by hand......
I dont know if i have explained to you what i have in mind effectively...
In my approach the assumption is that the coin has very little rotational speed..
In your approach the assumption is what is there in my approach and that the coin can be flipped in any way (not like it is flipped when we toss in cricket!!! like the flipping could be parallel to the axis of the "cyllindrical" part!!!)
1yaar i just making sure sure that it is a problem of continous things so dimension vise u can get angle by angle or area by area but by taking angles one is considering rotation havin a defined axis which is not here in the question or as if i have understand the problem
9gagar i couldnt understand ur approach please exp if possible thanks
1iam considering the surface area and than ks i got the the point it shouldbe 2Ï€rd/(2Ï€r2+2Ï€rd)=1/3
so d=r/2 now it sould be my ans (i think so)
62
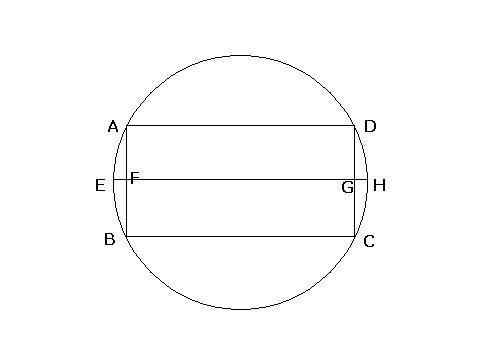
This is the top view Keeping the cyllindrical part on the ground....
gaurav, you are taking the area of such a cyllinder.... ABCD..
actually you should be taking the area of the part AEBCHD... which is the corresponding curved part...
It gives the same answer as what i am getting by my approach...
AEB=R. theta (theta is the arc length divided by radius)
area = 2pi. AEB (arc)
ratio has to be 1/3
so i am getting the cetral theta to be 1/3
hence the asnwer that i am getting...
(Sorry if i did not understand the approach that you have taken...)
could u give ur approach if that is the case?
1now thinking about ur ans nishant u are looking more correct because if u flip a coin by ur hand it must contain a axis by which it is rotating but i think this thing has to be clear before we should start solving the problem
62gaurav.. now i have a feeling that my answer will work even without flipping the coin..
and that was only after i saw your approach..
that is why i said that i liked ur approach more :)
62but then aditya thinks that the answer is none of our approach!! :(