very well kalyan....lets wait and see more
if /z/ = max{ /z-1/ , /z+1/ } then, 1./z+conjugatez/=1\2
2.z+ conj. z =1
3./z+conj.z /=1
4.none
i got the answer to be b and c
solution....
|z| = max{ /z-1/ , /z+1/ }
or x2 +y2=max{(x-1)2 + y2 , (x+1)2+y2}
so seeking the graph of y=x+1/x-1
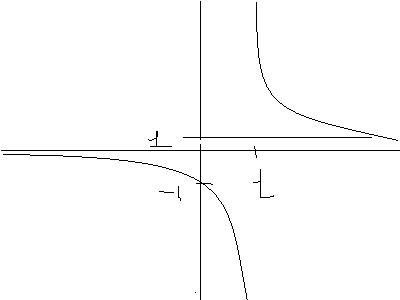
so when x>1
x2=(x+1)2....which gives absurd result....so
x<1 and x2=(x-1)2...which gives x=1/2
so x=1/2 i +c j where c is a real no.
So the answr comes out to be b and c......
-
UP 0 DOWN 0 0 13

13 Answers
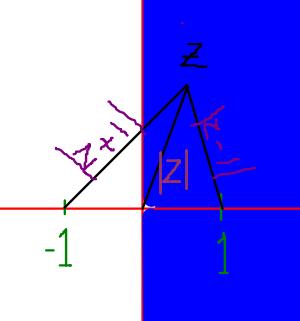
Consider z in the blue side, |z+1| should be equal to |z|, since |z+1|>|z-1|
and on the white side, |z-1|=|z|, using the same condition....
In either case, it is only possible, when z=±∞,±(∞±∞i)
This can be arrived at, by commonsense by looking at the graph or even arithmatically
On the y axis, |z+1|=|z-1| which is never equal to|z|,
I dont think any such complex number exists.....
My answer....D
[339]
I think what kalyan has done is correct!
Or is it one of your googleees' ? ;)
but Nishant bhyah plz see my solution.....in the hidden part....i got b and c
The question seemed very clear, at the first look....
Though I couldnt understand grandmaster's answer....
grandmaster, could U elaborate on ur answer??
@kalyan what i did was that i treated it algebrically..
or x2 +y2=max{(x-1)2 + y2 , (x+1)2+y2}
and then took cases..
and one obvious thing...did not include y2 anywhere...(as its in both Lhs and rhs)...
next i found where...(x+1)2/(x-1)2 is greater than 1(see graph)...and then equated x=(x+1)2 and x=(x-1)2 accordingly
i got x=1/2 i +c j where c is a real no. which seems to be an odd answer,nobody got it
Dude, jus' checked today,
Following ur method,
|z|=max(|z-1|,|z+1|)
taking |z|=x2+y2
Our condition, x2+y2=max{(x+1)2+y2,(x-1)2+y2}
Which is same as, x2=max{(x+1)2,(x-1)2}
I din understand the need of yer graph here. Considering y=(x+1)/(x-1) at x=-1, y=0, which doesnt hold good in your graph, proving an error!!!
Clearly, (x+1)2>(x-1)2 when, x>0, as |x+1|=|x-1| when x=0, and |x+1|>|x-1| when, x>0
Now taking cases,
When, x>0
x2=(x+1)2
=> x=-1/2, Not feasible!!
When, x<0
x2=(x-1)2
=>x=1/2, again not feasible
when x=0, we get 0=1 in either case, again no solution.....
So ultimately, there is no such complex number!!!
Answer, D[4]
[339]
lzl=max{lz-1l,lz+1l}
For Re(z)>0
=>lzl=lz+1l
=> Re(z)=-1/2
*edited*
=> No soln for Re(z)>0
*/edited*
For Re(z)<0
lzl=lz-1l
=>Re(z)=1/2
*edited*
=> No soln for Re(z)<0
So no solution for all real values of z
=> d)
*/edited*
@eureka 123
"For Re(z)>0
=>lzl=lz+1l
=> Re(z)=-1/2
For Re(z)<0
lzl=lz-1l
=>Re(z)=1/2"
Dont U find anything wrong here[7][7][7]
I already showed that in my previous post!!!
Rather, as per me ur solution turns out to be this.......
lzl=max{lz-1l,lz+1l}
For Re(z)>0
=>lzl=lz+1l
=> Re(z)=-1/2
Not in the taken domain
For Re(z)<0
lzl=lz-1l
=>Re(z)=1/2
Not in the taken domain
Again, no solution
Answer D [2][3][4][5][6][7][9]
Arrey U R taking Re(z)>0 and taking Re(z)=-1/2
Ye thodi chalta hai,
the eqn U took only holds good wen Re(z)>0
phir Re(z)=-1/2 kaise hoga??
Never mind dude, even I got a bit confused after looking at grandmasters soln.
The question was easy, but the solution was a bit odd!!