is d ans 49
A train has to stop at any 3 stations in the shown fixed lot such that no two stations are adjacent. Find the number of ways this is possible.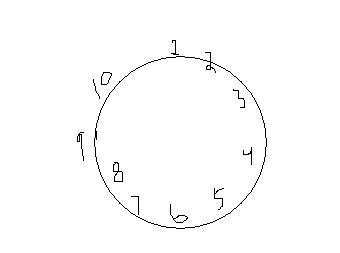
-
UP 0 DOWN 0 1 10

10 Answers
may be very bad a method but i like this...donno if it fits in here but have a look...
first of all i ll solve the problem in which it is not circular permutation but linear one...and then try to make it circular...[1][1][1]
let the train stop at 3 stations such that s1<s2<s3
now given condition, the trains cannot stop in adjacent station...
so, from the problem we have..
1≤s1
s1+2≤s2
s2+2≤s3
s3≤10
but its like hell if we try to solve these inequations and try to find the no of solutions (s1,s2,s3)
so instead we ll convert these to an equation...
so they yeild to,
1+a=s1
s1+2+b=s2
s2+2+c=s3
s3+d=10
where a,b,c,dε[0,∞)
adding the above four equations we get,
1+a+2+b+2+c+d=10
or, a+b+c+d=5
now trying to find no of solutions of s1,s2,s3 from the inequations is equivalent to finding possible set of value of a,b,c and d...
we have to partition the no 6 to give 4 nos using 3 partitions
so no of ways is 8C3
so the train can stop in 8C3 ways...[1][1][1]
if i did not go wrong anywhere..
neways this was the soln if the station were nt in circular arrangement...so now i ll try to delve into the actual problem!!
two cases...frst wen train stops at 1 and second the train doesnt
wen train stops at 1
let s1=1
so next it has to stop newhere from station 3 to station 9
in two positions,
so
3≤s2
s2+2≤s3
s3≤9
whch boils down to
a+b+c=4.........[jumping many steps[3][3]]
no of ways is 6C2..
wen train doesnt stop in 1
its a linear permutation in which all the three stations will lie within 2 to 10
so no of ways after solving this will be
7C3 most probably...
so total no of ways is 6C2+7C3=15+35=50
and i am completely unsure wether or not answer is correct!!
some expert please help!
thanks!
Elementary method:
total number of ways of train stopping in any 3 stations: 10C3
Subtract from this the number of invalid selections...
1 2 3
2 3 4
3 4 5
4 5 6
6 7 8
8 9 10
9 10 1
10 1 2
so 10 invalid selection-----------------1
then, count up the rest
1 2 4
1 2 5
1 2 6
1 2 7
1 2 8
1 2 9
...total 6 selections...doing the same for (2,3) (3,4)...until (10,1)...total number of invalid selections of this type would be 60------------------2
therefore total number of ways in which train can stop at 3 nonadjacent stations is :10C3 - 10 - 60=50
this is a nice question indeed and the solutions are also nice ones...