21Answer for the first one is indeed (c)
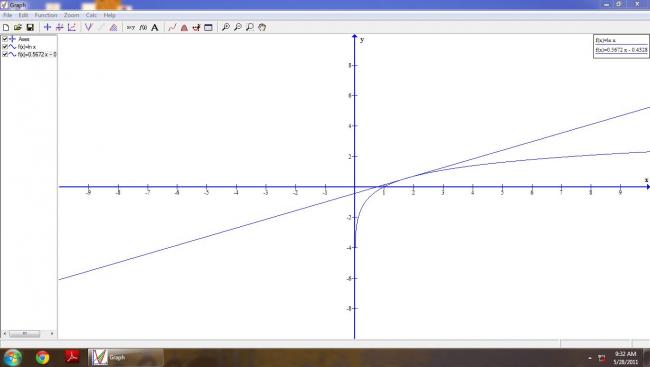
The minimum value of k is about 0.5672.
I am showing you the thing happening.
the line is then f(x) = 0.5672x - 0.4328
@ post 4:btw there is way easier way (if correct) to do that ;)
1. Maximum no. of real solutions for the equation axn+x2+bx+c = 0 , where a,b,c ε R and n is even positive no :
a) 2 b) 3 c) 4 d) None
2. The graphs y = 2x3-4x+2 and y = x3+2x-1 intersect exactly at 3 distinct points, then the slope of a line passing through any of these points is :
a) 2 b) 4 c) 6 d) 8
3. f(x) = -1+kx+k neither touches nor intercepts the curve y = ln x , then the minimum value of k ε :
a) (1/√e, e)
b) (e,e2)
c) (1/e , 1/√e)
d) None
-
UP 0 DOWN 0 0 17
17 Answers
21
341Q2) Alternative method.
Suppose the line is y = mx+c.
Then we have
2x^3-4x+2=mx+c \Rightarrow 2x^3 -(m+4)x+(2-c)=0
Similarly, from the other curve, we have
x^3 -(m-2)x+(1-c)=0
Since both polynomials have the same roots, the coefficients are proportional so that
2(m-2) = m+4 \Rightarrow m = \boxed{8}
Notice, we can obtain c also (as 4) and hence the line itself
106Q2. 2x3-4x+2 = x3+2x-1
=> x3-6x+3 = 0
if x1, x2, x3 are solutions then required slope is (note that x1 and x2 are arbitrary)
x13 + 2x1 - 1 - (x23 + 2x2 -1)x1 - x2
= (x12 + x22 + x1x2) + 2
= (x1 + x2)2 - x1x2 + 2
now x1 + x2 + x3 = 0
=> x1 + x2 = -x3 .... (1)
x1x2 + x3(x1 + x2) = -6
=> x1x2 = x32 - 6 ... (2)
using (1) and (2), slope
= x32 - (x32 - 6) + 2
= 8
21The condition of the problem will be fulfilled if and only if for all x>0
f(x) > lnx , ie. k-1+kx>lnx,ie. k>lnx+1x+1
consider g(x) = lnx+1x+1
g'(x) = 0 implies lnx = 1x
It can be checked that gmax ε (1/e , 1/√e) (tracing the exact value is quite impossible , i think,w/o wolfram alpha)
As we must have kmin → gmax , kmin lies in the interval (1/e , 1/√e)
62First one can be done by graph and equating
-ax^n = x^2+bx+c
what is evident is the left side will be a downward facing curve (rarely an upward facing one..)
(similar to the shape of a parabola if a is -ve)
Can you draw some conclusion..??
Else you could also try to use descartes rule of sign change...
You could also think of the derivative and use that if the 1st derivative has n roots then the original equation has atmost n+1 roots...
(Like to try on ur own?)
71Main toh third question mein why? tak pahuchne ke baad BOLD ho gaya tha!!
71@Subbhomoy
The Answer to third one i.e., (c) is correct.
Now for your query, that thing is ' any two of these points'
@Subhodip
I reached the same conclusion and you have for the problem 1, But in actually the answer is (d) None
Exp: I have this explanation for that. Put a = -1 and b=c=0, Hence Infinite Solutions!!. But should the sum really trick us into such things.?
Really noxious ... :(
49now I am half-expecting a comment from Pirtish on me about this thread :P
49for (2) is it any of these points or any two of these points?
493)
First easy realisation is f(x) is a straight line.
f'(x)=k
f(x) passes through (0,k-1)
let us consider the case for tangent to y=ln x is parallel to f(x).
for that condition,
f'(x) = dydx
i.e. k = ddx(ln x) = 1x
i.e. x = 1k
and, y = ln(1k) = - ln k
So, the point on y=ln x the tangent at which point is parallel to f(x) is of the form (1k, -ln k)
thus, \frac{-ln k - (k-1)}{\frac{1}{k}-0}\leq k (why?)
gives: -ln k -(k-1) ≤ 1 (since k >0)
Or, k ≥ -ln k
for minimum value of k, k = -ln k
lets check for 1/√e , 1/e , e , e2
-ln(1/√e) = 1/2 <1/√e (since 2<e<3, So, √2 < √e <√3 < 2)
-ln(1/e) = 1 > 1/e
Thus, k>-ln k @ k=1/e
and k<-lnk @ k=1/√e
Thus somewhere between 1/e and 1/√e
k becomes equal to -ln k
Thus minimum value of k is some value between 1/e and 1/√e
Hence, (c) is the answer! [1] [1]
yeeeeeeeee!! I did it! :D
211) 4
2)wrong, i think. how can we find the slope with just a point ?
3)wrong again, i think.. how can the 'minimum' value form an interval !!!