11. its 66,i think
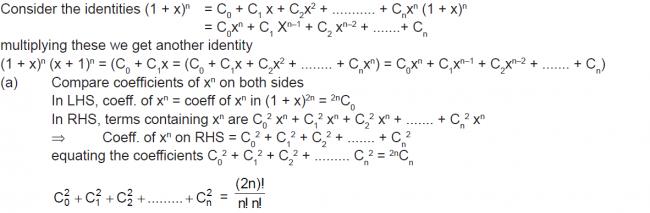
1)Number of ways 10 persons can take seats in a row of 24 fixed seats so that no two persons take consecutive seats is
2)C02 + C12 + C22 + .... + Cn2 =
3)C1+4.C2 + 7.C3 + ... + (3n-2).Cn =
4)Number of integral terms in the expansion (31/2 +51/3)1296 =
-
UP 0 DOWN 0 0 10
10 Answers
1057in question no 4 the answer is 217 as 1296-r shud be divisible by 2 and r shud be divisible by 3...
therefore r shud be divisible by 6....therefore 1296/6 terms...
this cums out to be 216 but we did not count for r to be 0....
so 217 terms....
2621) should be 66*10!
3) use the fact that nCr = nCn-r to sum up the series
3i think this can be done.
it will be C(2n,n).
try multiplying (1+x)n and (x+1)n
and compare the coefficients of the required terms...
3Q1)
how to do it???
i am getting a different answer./.
something to do with partitions.
12) better do it like this,
c02 + c12.....+cn2
= c0*cn + c1*cn-1 ....
= number of ways of selecting n objects out of 2n
= 2nCn
