Compleksh::::

JEE Advanced 2015 Papers › Algebra questions › Compleksh::::

let Z_r,r=1,2,3.....n are n distinct roots of eq ^{n}C_{1}x+^{n}C_{2}x^{2}+^{n}C_{3}x^{3}+.......^{n}C_{n}x^{n}=0 in argand plane.If der exist exactly one Z_r, rÎµ{1,2....n} such that arg\left(\frac{Z_{r}-(-1+\sqrt{2}i}{(-1)-(-1+\sqrt{2}i)} \right)=\frac{\pi }{4} then n can be ??

#Mathematics #Algebra

UP 0 DOWN 0 0 4
Post on FacebookPost anonymously?

4 Answers

341

Hari Shankar ·2010-01-15 21:04:50

pls check the denominator of the arg expression

UP 0 DOWN 0
Post on FacebookPost anonymously?

1

Che ·2010-01-15 21:14:30

i checked the denominator......no prob with it.

UP 0 DOWN 0
Post on FacebookPost anonymously?

1

Kalyan Pilla ·2010-01-15 21:47:47

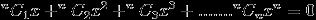is the same as (x+1)ⁿ=1

The solution to this lies on the red circle in the fig.

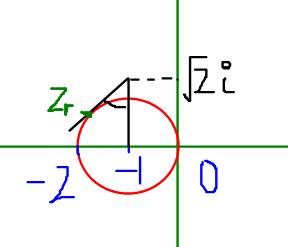
z_r is a point such that, arg(-1+√2i - z_r)=âˆ©/4

This when solved, along with the eqn of circle, |z+1|=1 or by using simple geometry gives z_r= e^i3âˆ©/4-1

This when substituted in the eqn gives, (e^i3âˆ©/4)^n/r=1

=> 3âˆ©n/4 = 2âˆ© , or n/r=8/3,

This gives n=8 and e^i3âˆ©/4-1 is the third root anti-clockwise...........

[339]

UP 0 DOWN 0
Post on FacebookPost anonymously?

1

Che ·2010-01-15 22:18:34

yes correct !

UP 0 DOWN 0
Post on FacebookPost anonymously?

Your Answer

Basic Integral Calculus Operators Symbols Matrix Cases

√ √ || {} [] () → ~ ^ x x x → → ln log lg lim lim cos sin tan cot arcsin arccos arctan

∫ ∫ ∫ ∫ ∫ ∬ ∬ ∬ ∬ ∬ ∭ ∭ ∭ ∭ ∭ ⨌ ⨌ ⨌ ⨌ ⨌

∑ ∑ ∑ ∑ ∑ ∮ ∮ ∮ ∮ ∮ ∏ ∏ ∏ ∏ ∏ ∐ ∐ ∐ ∐ ∐

+ - × ÷ ± ∓ = ∪ ∩ ≠ ∼ ≈ ∅ ∀ ∃ ∈ ∋ ∝ ≤ ≥ ≃ ≅ ≡ < > ≪ ≫ ⊂ ∉ ⊃ ⊆ ⊇ ⇒ ⇐ ⇔ ⇒ ⇐ ⇔ ⇑ ⇓ ⇕ → ← ↔ → ← ↔ ↑ ↓ ↕ ↖ ↗ ↘ ↙ ↪ ↩ ⇀ ↼ ⇁ ↽

° ∂ ∞ α β γ δ θ λ μ ν ξ π ρ σ φ ω ε ƒ κ τ υ Γ Δ Λ Σ Π Ω