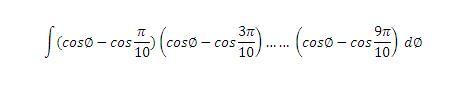1somone iska answer karo.
14 Answers
29@Gallardo...i guess he is asking for this integration
\int (cosx-cos\frac{\pi}{10} )(cosx-cos\frac{3\pi}{10}).....(cosx-cos\frac{9\pi}{10}) dx
1notice
cosx=-cos(pi-x)
now club the complements
to get
a^2-b^2 form
so will end up with three degree eq in cos^2x
(cos2x-α)(cos2x-β)(cos2x-γ)
=cos6x-(α+β+γ)cos4x+(αβ+γβ+αγ)cos2x-αγβ
now do integration
note: cos6x can be derived using cos6x formula
and cos4x can be derived using cos4x
cosnx=cosnx(1-nC2tan2x+nC4tan4x-.........)
341This is just \int \cos 5\phi \ d \phi = \frac{\sin 5 \phi}{5}+C
62uttara, see this question like this..
\int (x-a)(x-b)(x-c)(x-d)(x-e)dx
Where, \\a=\frac{e^{i\theta}+e^{-i\theta}}{2} \\b=\frac{e^{2i\theta}+e^{-2i\theta}}{2} \\c=\frac{e^{3i\theta}+e^{-3i\theta}}{2}
Now try..
1sir , but common difference is 2θ
so
2a=eiθ+e-iθ
2b=ei3θ+e-i3θ
2c=ei5θ+e-i5θ
.
.
.
.
then we can use viete's relatioon
341No, its much simpler.
Notice that \cos \frac{(2k-1) \pi}{10} ; 1 \le k \le 5 are the five distinct roots
to the equation \cos 5\theta = 0.
Now you perhaps know that \cos n \theta for any n can be expanded as a polynomial in \cos \theta of degree n and leading coefficient 2n-1
[This sequence of polynomials are named Chebyshev Polynomials.
See Trigonometric definition in http://en.wikipedia.org/wiki/Chebyshev_polynomials.
Otherwise notice that \cos \n \theta + \cos (n-2) \theta = 2 \cos (n-1) \theta \cos \theta) and use strong induction to prove this statement]
So, \cos 5 \theta = P(\cos \theta) = 2^{n-1} \prod_{k=1}^5 \left(\cos \theta - \cos \frac{(2k-1) \pi}{10} \right)
Hence the given expression equals \frac{\cos 5 \theta}{16}
and the integral \frac{\sin 5 \theta}{80} + C
(Note how shamelessly I have changed the answer :D)
1east or west
Mr.prophet is the best
but how is that 2n-1 is coming
and can that polyomial be proved using this
cosnx=cosnx(1-nC2tan2x+nC4tan4x-.........)
1i got it sir
\cos{n\theta }=\cos^n\theta \left(1-\binom{n}{2}\tan^{2}\theta +\binom{n}{4}\tan^{4}\theta+............ \right)\\ \cos{n\theta }=\left(\cos^n\theta -\binom{n}{2}\sin^{2}\theta \cos^{n-2}\theta +\binom{n}{4}\sin^{4}\theta \cos^{n-4}\theta +............ \right)\\ put \ \sin^2\theta=(1-\cos^2\theta ) \\ \text{we will get coefficeint of } \cos^n \theta =\frac{1+\binom{n}{1}+\binom{n}{2}+.......\binom{n}{n}}{2}\\\left(\text{taking in consideration that}\binom{n}{r}=\binom{n}{n-r} \right)\\ =2^{n-1}
prophet sir is it right ?
and i hpe the other degrees are also having same coefficient
as it is obvious from symmetry and the signs will oscillate
1thank you PROPHET SIR for the solution , sir i have gone by Chebyshev Polynomials and its roots but still not know how is the coefficient of cosnx is 2n-1.
341That's what I asked you to prove using induction.
Consider the sequence \{a_n\} given by a_n = \cos n \theta
From the trigonometric relation in the previous post, this sequence satisfies the equationa_n + a_{n-2} = 2 a_{n-1} a_1
Our hypothesis is two-fold:
1) an can be expresssed as a polynomial of degree n in a1 for all n (recall that a_1 = \cos \theta)
2) The coefficient of \cos ^{n} \theta i.e a_1^n is 2^{n-1}
Now, we use strong induction to prove this. So, after verifying the statement for n=1, 2 let's assume that the above are true for all n≤k. Now lets prove the statement for n=k+1.
We have using the equation a_{k+1} + a_{k-1} = 2a_ka_1
Write this as a_{k+1} = 2a_ka_1- a_{k-1}. Its easy to see that RHS is a polynomial of degree n in a1 with leading coefficient 2k
From the induction hypothesis, ak is a polynomial of degree k with leading coefficient 2k-1. Of course ak-1 is of degree k-1 and does not have any further role.
So its immediately apparent that our hypothesis is proved for n=k+1 and hence is true for all natural numbers.