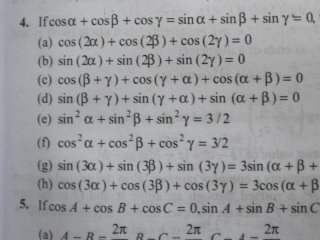let Z=ei(α+β+γ)=0
therefore, cosα+cosβ+cosγ=0 & sinα+sinβ+sinγ=0
Z2=0(Z=0)
therefore, e2i(α+β+γ)=0
or ei(2α+2β+2γ)=0
therefore, cos2α+cos2β+cos2γ=0 & sin2α+sin2β+sin2γ=0
Since,ei(2α+2β+2γ)=0
therefore, ei{(α+β)+(b+γ)+(γ+α)}=0
So. cos(α+β)+cos(b+γ)+cos(b+γ)=0 & sin(α+β)+sin(b+γ)+sin(γ+α)=0
 Himanshu Giria thanx ... quite a small method .....
Upvote·0· Reply ·2014-02-06 17:47:53
Himanshu Giria thanx ... quite a small method .....
Upvote·0· Reply ·2014-02-06 17:47:53 Aditya Agarwal i dont think this is correct.
e^[i(2α+2β+2γ)] should be equal to cos(2α+2β+2γ) and so on and so forth...
Aditya Agarwal i dont think this is correct.
e^[i(2α+2β+2γ)] should be equal to cos(2α+2β+2γ) and so on and so forth...