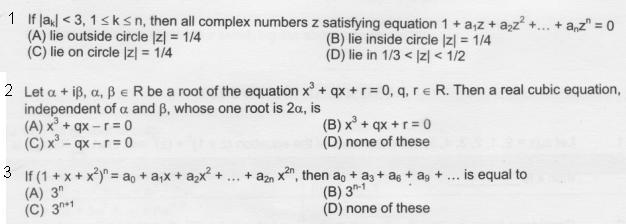Complex Number

\hspace{-16}\bf{(2)\;\; }$ If $\bf{\alpha+i\beta}$ be the Roots of a Cubic equation, Then $\bf{\alpha-i\beta}$\\\\ will also the Roots of a Given Equation.\\\\ Let Third Root of a Given equation is $\bf{\gamma}$. Then Using Vieta,s formula....\\\\ $\bf{\alpha+i\beta+\alpha-i\beta+\gamma=0\Leftrightarrow \gamma=-2\alpha............(1)}$\\\\ $\bf{\left(\alpha+i\beta\right).\left(\alpha-i\beta\right)+\left(\alpha-i\beta\right).\gamma+\left(\alpha+i\beta\right).\gamma = q}$\\\\ $\bf{(\alpha^2+\beta^2)+2\gamma.\alpha=q\Leftrightarrow (\alpha^2+\beta^2)=q-2\alpha.\gamma=q+4\alpha^2......(2)}$\\\\ $\bf{\left(\alpha+i\beta\right).\left(\alpha-i\beta\right).\gamma=-r}$\\\\ $\bf{(\alpha^2+\beta^2).\gamma=-r\Leftrightarrow (\alpha^2+\beta^2)=-\frac{r}{\gamma}=\frac{r}{2\alpha}.......(3)}$\\\\ from $\bf{(2)}$ and $\bf{(3)}\;,$ We Get\\\\ $\bf{q+4\alpha^2 = \frac{r}{2\alpha}\Leftrightarrow (2\alpha)^3+q(2\alpha)-r=0}$\\\\ So $\bf{2\alpha}$ is a Root of $\bf{x^3+qx-r=0}$

\hspace{-16}\bf{(3)\;\; }$ Here Given.......\\\\ $\bf{(1+x+x^2)^{n}=a_{0}+a_{1}.x+a_{2}.x^2+a_{3}.x^3+................+a_{2n}.x^{2n}}$\\\\ Put $\bf{x=1}$\\\\ $\bf{3^n=a_{0}+a_{1}+a_{2}+a_{3}+............+a_{2n}.........................................(1)}$ \\\\Put $\bf{x=\omega\;\;}$ and $\bf{x=\omega^2}$\\\\ Where $\bf{\omega}$ is a Cube Root of Unity and $\bf{\omega^{3n}=1\forall n\in \mathbb{Z}}$ and $\bf{1+\omega+\omega^2 = 0}$\\\\ $\bf{(1+\omega+\omega^2)^n=a_{0}+a_{1}.\omega+a_{2}.\omega^2+a_{3}.\omega^3+...........+a_{2n}.\omega^{2n}.....(2)}$\\\\ $\bf{(1+\omega^2+\omega)^n=a_{0}+a_{1}.\omega^2+a_{2}.\omega^4+a_{3}.\omega^6+...........+a_{2n}.\omega^{4n}.....(3)}$\\\\ Now $\bf{(1)+(2)+(3)\;,}$ We Get\\\\ $\bf{3^n+0+0=3a_{0}+3a_{3}+3a_{6}+3a_{9}+.............}$\\\\ $\bf{3^{n-1}=a_{0}+a_{3}+a_{9}+...................}$

\hspace{-16}\bf{(1)\;\; }$ Here Given $\bf{\mid a_{r} \mid<3\; \forall \; 1 \leq k \leq n.....}$\\\\ and $\bf{1+a_{1}.z+a_{2}.z^2+..............+a_{n}.z_{n}^n = 0}$\\\\ $\bf{-1=a_{1}.z+a_{2}.z^2+..............+a_{n}.z_{n}^n}$\\\\ Taking Modulus on both Side......\\\\ $\bf{\mid - 1 \mid = \mid a_{1}.z+a_{2}.z^2+..............+a_{n}.z_{n}^n\mid}$\\\\ Now Using $\bf{\triangle}$ Inequality, We Get\\\\ $\bf{\mid a_{1}.z+a_{2}.z^2+..............+a_{n}.z_{n}^n\mid\leq \mid a_{1}z\mid+\mid a_{2}z^2\mid+\mid a_{3}z^3\mid+...........+\mid a_{n}z^n\mid \leq \mid a_{1}z\mid+\mid a_{2}z^2\mid+\mid a_{3}z^3\mid+...........+\mid a_{n}z^n\mid }$\\\\ Now $\bf{\mid a_{1}z\mid+\mid a_{2}z^2\mid+\mid a_{3}z^3\mid+...........+\mid a_{n}z^n\mid = \mid a_{1}\mid.\mid z \mid+\mid a_{2}\mid.\mid z \mid^2+.........+\mid a_{n}\mid.\mid z \mid^n}$\\\\ So $\bf{1<3\mid z \mid+3\mid z \mid^2+.........+3\mid z \mid^n...........(1)}$\\\\ Now There are Two cases::\\\\

\hspace{-16}$$\bf{Case\; (1)::}$ When $\bf{\mid z \mid <1\;}$ Then\\\\ Using $\bf{G.P}$ Series Sum in eqn (1)......\\\\ $\bf{1<3\frac{\mid z \mid }{1- \mid z \mid}\Leftrightarrow \mid z \mid >\frac{1}{4}}$\\\\ Similarly.......\\\\ $\bf{Case\; (2)::}$ When $\bf{\mid z \mid \geq 1\;}$ Then\\\\ equation....$\bf{(1)}$ is always valid.\\\\ So Final answer is $\bf{\mid z \mid }$ does Not lie in the Interior of $\bf{\mid z \mid =\frac{1}{4}}$