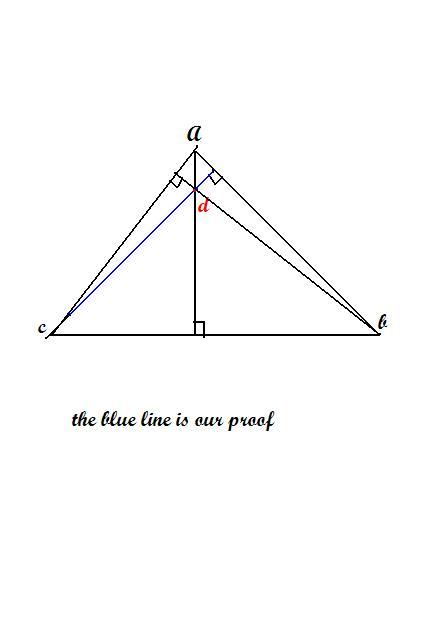
66Let A, B, C be the geometric image of the complex numbers a, b, c. And let D be the orthocenter of triangle ABC. Then assigning the complex number d to D satisfies the given first two conditions and the third one easily follows.
Good prob flicked from another forum:
Given complex numbers a,b,c,d such that \frac{a-d}{b-c} and \frac{b-d}{c-a} are purely imaginary, prove that \frac{c-d}{a-b} is also purely imaginary
-
UP 0 DOWN 0 1 4
4 Answers
66
1yres sir i got it
threee points are used to form a triangle
and the fact that altitudes are concurrent
sir am i right ?
