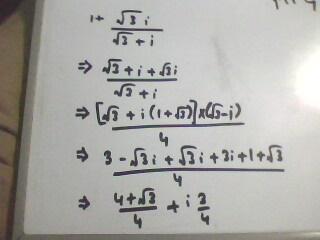complex numbers

{\color{red}Given \ z=\frac{\sqrt3+i}{2}}

\Longrightarrow z=cos(\frac{\pi}{6})+isin(\frac{\pi}{6}) \\ z^{102}=cos(\frac{102\pi}{6})+isin(\frac{102\pi}{6}) \\ z^{102}=-1 \Longrightarrow z^{101}=\frac{-1}{z} \\ \text{Subsitute in the given expression} \\ (\frac{-1}{z}-i)^{105} \\ \\ \text{Take minus common} \\ \Longrightarrow (-1) (\frac{1+zi}{z})^{105} \\ \text{Substitute the value of z,After simplification,we will get} \ (-1)z^{105} \\ \Longrightarrow (-1)z^{102}z^{3} \\ \Longrightarrow z^3

aacha koi ni try d way i id may b m makin sum cal mistake
z=(i+√3 )/2 zi= w^2..............
.. (or w.........m confused :( )

so then (z¹⁰¹ +i¹⁰³ )¹⁰⁵

isse solve karo

o aapko aara hai kya answer ?

nahiin ji answer z³ hain

soln for iⁱ question

i= (e^{iÎ /2})ⁱ =e^{-Î /2}

z^2

yeh hi toh answer hai arey A aur B poche hai :P

ha anuj post karna

integration definite hai.........i mean she'z correct...............shall i post whole solution???????

for 1t Q

one of the values of iⁱ is

a]e^{-Î /2}

b]e^{Î /2}

c]e^Î

d]e^-Î

1+ω+ω²=0 therefore ge =(-ω²)⁷
=-ω¹⁴ =-ω²
=1+ω=A+Bω

A=B=1

Hey Matie, inte : PL. see c this :

http://targetiit.com/iit_jee_forum/posts/sum1_pl_explain_this_2me_3321.html

hey sorry re doin
i wrte 21 on ma paper n took taht as 4 woh 4 ki atrh dikh ra tha

A= 1 AUR B=1 tapan tujhe?

arctan(3/(4+√3)
=27.626°
wats da ans?

nahiin

options hai kya

2] if ω is a complex cube root of unity, and

\large \left(1+\omega \right)^{7}=A+B\omega

then A and B are respectively --------------