Now you have proved that all members of (A∩B)c are members of Ac union Bc.
But don't we want to prove the converse statement also ?
In a book, the proof for demorgan's law,
(A∩B)* = A*unionB*
[*=complement]
starts with,saying that for all x belongs to (A∩B)* , x is not a member of AunionB.
But how can we say that, for example,
if A = {1,2,3} and B = (2,3,4,5} and U = {1,2,3,4,5}
(A∩B)^ = {1,4,5}
and AunionB = {1,2,3,4,5}
here all x which belongs to (A∩B)* are members of the set AunionB.
-
UP 0 DOWN 0 0 4

4 Answers
Vivek @ Born this Way
·2010-11-05 08:27:20
(A∩B)* , x is not a member of AunionB
I think it should have been like this : "for all x ε (A∩B)c , x is not a member of A∩B"
Which book it is?
Don't panic, I'll supply the proof too: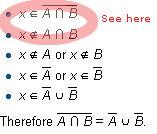
johncenaiit
·2010-11-05 09:24:30
avisikta(rai)
·2010-11-05 20:17:53
x is not a member of A union B...n dis becums more easy if we prove it by venn diagram(s)...