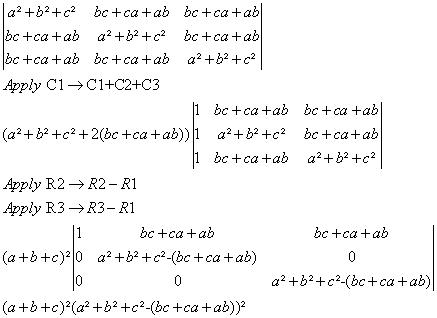1Can it be zero too?
\hspace{-16}$Show that $\mathbf{\begin{vmatrix} a^2+b^2+c^2 &bc+ca+ab &bc+ca+ab \\\\ bc+ca+ab &a^2+b^2+c^2 &bc+ca+ab \\\\ bc+ca+ab &bc+ca+ab & a^2+b^2+c^2 \end{vmatrix}}$\\\\\\ is always Positive \;, Where $\mathbf{a\;,b\;,c}$ are distinct real no.
-
UP 0 DOWN 0 1 5
