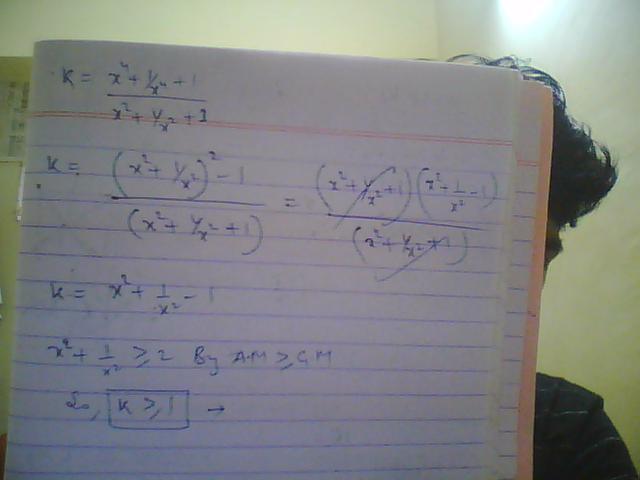sir,i did i like this............
\frac{(x^{4}+\frac{1}{x^{4}}+1)}{(x^{2}+\frac{1}{x^{2}}+1)}
in this expresion as we can see the optimum is attained x=1...
thats 3/3=1..coz..when x>1...we can see numerator is bigeer than denominator.....hence k will bcom big and big.......
wen x<1.......agin numerator >denominator...as now the 1/x^4 factor plays the role.......we need not bother as x<0 as function is even....if we have proved for +ve part, the same holds good for the negative also
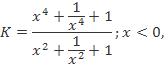
which of the following intervals best describes the range of K?
1. (1/2, ∞)
2. (1, ∞)
3. (1/4, ∞)
4. [1, ∞)
5. (3/4, ∞)
-
UP 0 DOWN 0 0 7

7 Answers
K=\frac{x^{4}+ \frac{1}{x^{4}}+ 1}{x^{2} + \frac{1}{x^{2}} + 1 }
numerator= \left( x^{2}+ \frac{1}{x^{2}}\right) ^{2} -2 + 1
numerator= \left( x^{2}+ \frac{1}{x^{2}}\right) ^{2} -1
using a2 -b2 = (a+b)(a-b)
numerator= ( x^{2}+ \frac{1}{x^{2}} -1 )(x^{2} + \frac{1}{x^{2}} + 1)
Thus:
K=\frac{ \left( x^{2} + \frac{1}{x^{2}} + 1\right) \left( x^{2} + \frac{1}{x^{2}} - 1 \right) }{x^{2}+ \frac{1}{x^{2}}+ 1}
Thus\; K = ( x^{2}+ \frac{1}{x^{2}} -1 )\; \; \;
we\; can\; cancel\; the\; term\; x^{2} + \frac{1}{x^{2}} + 1\; since\; it\; can\; never\; be\; zero
also \; x^{2}\; can\; also\; never\; be\; zero\; since\; x<0\;
since we can multiply by x2 thus\; x^{4}-x^{2}(k+1)+1 =0
then\; use\; discriminant \geq 0\; and\; neglect\; -ve\; value\; of k\; , is\; it\; correct\;??
@ qwerty u r corect till here K=x^2 +\frac {1}{x^2} -1
but after this make it simpler
Since x2 and 1/x2 >0 always
so from AM-GM x^2+\frac {1} {x^2} \geq 2
=> (x^2+\frac {1} {x^2} -1)\geq 1
=>K\geq 1
i just keep forgetting thta important property of AM-GM [16]
btw tnx for reminding ...