23answer is 467
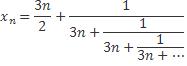
and yn = xn*xn
Then what is the value of y1 + y2 + y3 + y4 + y5 + y6 + y7 + y8?
1. 459
2. 259
3. 257
4. 467
5. None of these
-
UP 0 DOWN 0 1 3
3 Answers
23x_{n} = \frac{3n}{2} + \frac{1}{3n + \frac{1}{3n + ...}}
x_{n} = \frac{3n}{2} + \frac{1}{\frac{3n}{2} + \frac{3n}{2}+ \frac{1}{3n + ....}}
x_{n} = \frac{3n}{2} + \frac{1}{\frac{3n}{2} + x_{n} }
x_{n}\left( \frac{3n}{2} + x_{n}\\ \right) = \frac{3n}{2}\left(\frac{3n}{2} + x_{n}\\ \right) + 1
ON solving further we get
x_{n}^{2} = \frac{9n^{2}}{4} + 1 = y_{n}
\sum_{n = 1 }^{8}{y_{n}} = \frac{9}{4} \left(8\times 9\times 17 \right)/ 6 + 8
\sum_{n = 1 }^{8}{y_{n}} = 467
