Let a, b, c, d, e be real numbers satisfying
a+ 16b+ 81c + 256d + 625e = 1
16a + 81b + 256c + 625d + 1296e = 12
81a + 256b + 625c + 1296d + 2401e = 123
256a + 625b + 1296c + 2401d + 4096e = 1234
625x1 + 1296x2 + 2401x3 + 4096x4 + 6561x5 = 12345
What is 1296a + 2401b + 4096c + 6561d + 10000e?
11The Lagrange interpolating polynomial is the polynomial P(x) of degree <=(n-1) passing through the n points (x_1,y_1=f(x_1)), (x_2,y_2=f(x_2)), ..., (x_n,y_n=f(x_n)), and is given by
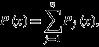
P(x) = ((x-x_2)(x-x_3)...(x-x_n))/((x_1-x_2)(x_1-x_3)...(x_1-x_n))y_1+((x-x_1)(x-x_3)...(x-x_n))/((x_2-x_1)(x_2-x_3)...(x_2-x_n))y_2+...+((x-x_1)(x-x_2)...(x-x_(n-1)))/((x_n-x_1)(x_n-x_2)...(x_n-x_(n-1)))y_n.
the answer looks correct.
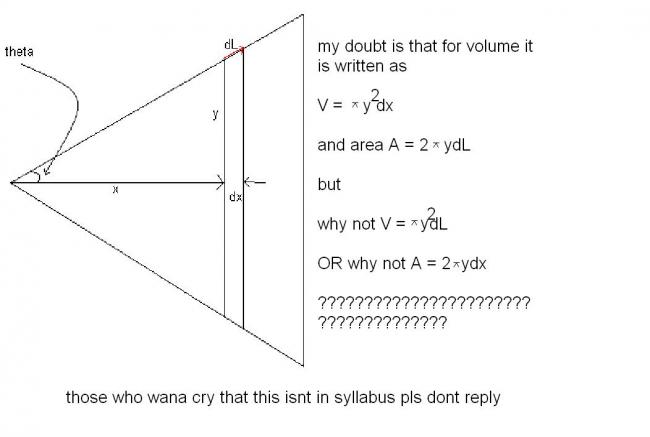
1For VOLUME;
you use the other formula (provided X and Y axis should be taken into consideration)
1but that question can be solved without LAGRANGE INTERPOLATION FORMULA;
just bt writing
(k+5)5 =A(k)5+B(k+1)5 +C(k+2)5 +D(k+3)5 +E(k+4)5
and by comparing the coeff ;solve for A,B....E
A=1
B=-5
C=10
D=-10
E=5
1method given by prophet sir in this topic(lagrange interpolation formula ) also isnt in jee syllabus , so why not answer my question too ? wich is actually relevant to jee .............. [1]
341Oh! sorry, I was making a back-of-the-envelope calculation, so wasnt really checking. thanks for fixing that.
1the ans is :
1 − 5 * 12 + 10 * 123 − 10 * 1234 + 5 * 12345=50556
1prophet sir please answer here it is my sincere request pleaseeeeeeeeeeeeeeeeeeeeee
i beg to u http://www.targetiit.com/iit-jee-forum/posts/area-volume-18431.html
http://www.targetiit.com/iit-jee-forum/posts/area-volume-18431.html
1@prophet sir,i have no idea of Lagrange interpollation formula,
:
and the ans is incorrect,but i think u have made a mistake here:
1-60+1230-12340+""12345""
341Let
P(x) =ax^4+b(x+1)^4+c(x+2)^4+d(x+3)^4+e(x+4)^4
We have P(1) =1, P(2)=12,.., P(5)=12345.
By Lagrange Interpolation Formula, we have
P(x) = \frac{(x-2)(x-3)(x-4)(x-5)}{24}P(1) - \frac{(x-1)(x-3)(x-4)(x-5)}{6} P(2)+ \\ \\ \frac{(x-1)(x-2)(x-4)(x-5)}{4} P(3) - \frac{(x-1)(x-2)(x-3)(x-5)}{6} P(4) + \\ \\ \frac{(x-1)(x-2)(x-3)(x-4)}{24}P(5)
We are asked to find P(6) which is obtained as
1-60+1230-12340+12345 =1176
71Lol.. exactly maine bhi yehi guess kiya tha.. lekin agar yehi answer hota toh shayad woh itni mehnar se likhkar post karta kya?
