Given that x^3-3xy^2 = 10 and y^3-3x^2y = 30 find the value of x^2+y^2
1subtracting both equations..........
(x-y)^{3}=(-20)
(x-y)=(-20)^{\frac{1}{3}}
(x-y)^{2}=(20)^{\frac{2}{3}}
x^{2}+y^{2}-2xy=(20)^{\frac{2}{3}}
let xy be k1,and x2+y2=k2
expanding first equation.....
-(20)1/3.(k1 + k2) -3k1k2=-20..(1)
k1 -2k2=202/3
putting k1=202/3+2k2 in (1)
we get x2 +y2=1/2(202/3-201/3)
341that's correct(a pink to xyz!).
But there's an easier solution. So this thread's still open
341(x+iy)^3 = (x^3-3xy^2)+i(3x^2y-y^3) = 10 - 30i \\ \\ \Rightarrow x^2+y^2 = |x+iy|^2 = |10-30i|^{\frac{2}{3}} = 10
11Nice soln Prophet sir.....I applied Geometry to this.....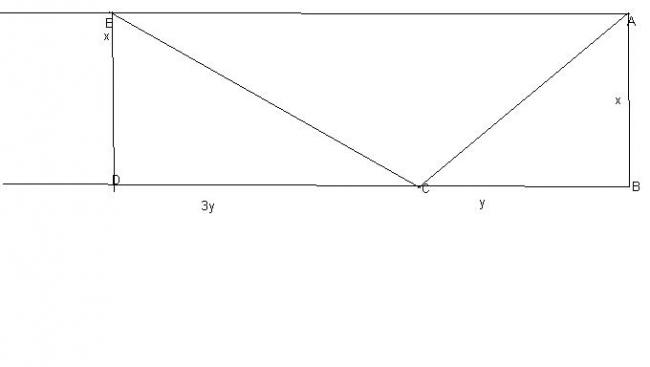
Let Angle ACB be \theta so I have \frac{x}{y}=tan\theta Putting this in the above equations and dividing them, I have tan3\theta=\frac{-1}{3}.....
Now in triangle ECA,
\frac{\sqrt{x^2+y^2}}{sin3\theta}=\frac{4y}{sin2\theta}
Also I know \frac{y}{\sqrt{x^2+y^2}}=cos\theta
From which I have sin^2\theta=\frac{5}{8}\Rightarrow 3x^2=5y^2
x^2+y^2=\frac{8y^2}{3}
Putting x2=5y23 in 2nd eqn, we can get y, and can get \frac{8y^2}{3} as well......Done.
