341I was looking for all roots. Your method is nice.
There is an alternative method. Hint: trig substitution
8 Answers
1lets \ consider \ \\ P(x)=4x^2(x^4 -\frac{3}{2}) \\ P(x)=4x^2(x+(\frac{3}{2})^{\frac{1}{4}})(x-(\frac{3}{2})^{\frac{1}{4}})(x^2+(\frac{3}{2})^{\frac{1}{2}}) \\ roots \ are \ 0,0 ,+(\frac{3}{2})^{\frac{1}{4}},-(\frac{3}{2})^{\frac{1}{4}}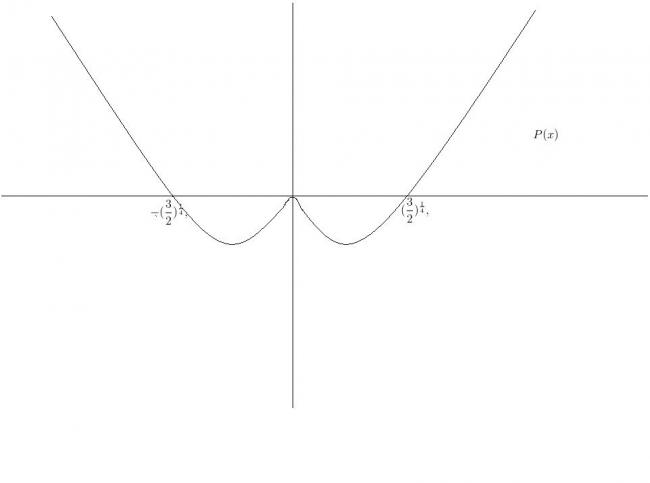
now \ putting \ P'(x) =0 \ we \ can \ find \ those \ peaks \\ P'(x)=24x^5 -12 x=0 \\ x=0 \ is \ obvious \ from \ graph \\ x_0 =(\frac{1}{2})^{\frac{1}{4}} \\ P(x_0)= \sqrt{2} - 3\sqrt{2} =-2\sqrt{2} \\ now \ adding \ a constant\ means \ dragging \ the \ graph \ along \ y \ axis \\ so \ we \ see \ exactly \ two \ roots \ are \ there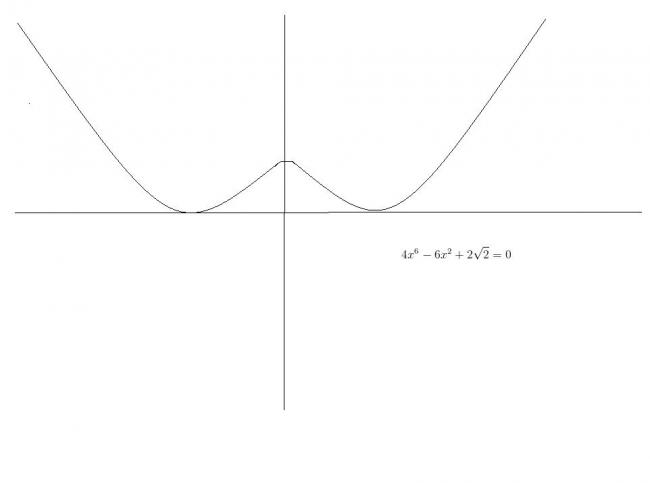
roots \ are \\ (\frac{1}{2})^{\frac{1}{4}},-(\frac{1}{2})^{\frac{1}{4}}
341
11I thought of the substitution
x^2=a...
So on dividng by 2, we finally have 2a^3-3a+\sqrt{2}=0
From which the factorisation (2a^2-2\sqrt{2}a+1)(a+\sqrt{2})=0 follows.
(\sqrt{2}-a)^2=0 \Rightarrow x=\sqrt[4]{2}
Also complex roots are \sqrt[4]{2}i...
341Ok, I had not thought of that.
But moving on from Soumik's first substitution x2=a,
we get 2a^3-3a+\sqrt 2 = 0
Now, when you see a3 and 3a etc. , there's just the possibility that a sin 3x substitution is possible.
So letting a = \sqrt 2 \sin y and dividing by √2 throughout you get
sin 3y = 1
and the roots are then got very easily