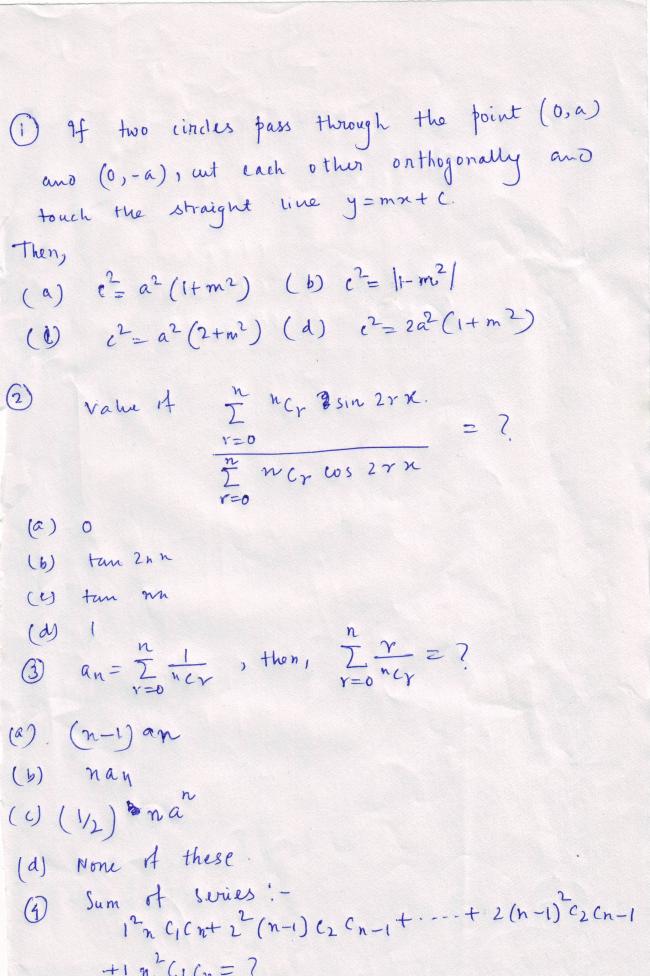1let \: S= \sum{\frac{r}{C_{r}}}
\frac{r}{C_{r}}+\frac{n-r}{C_{n-r}}= \frac{r}{C_{r}}+\frac{n-r}{C_{r}}= \frac{n}{C_{r}}
thus \: 2S= \sum{\frac{n}{C_{r}}} = na_{n}
8 Answers
1
1consider the following expansion
\cos 2n x+ \iota \sin 2n x=\sum{^nC_r\cos 2rx}+\iota\sum{^nC_r\sin 2rx}
compare real and imaginary parts now
hence answer is
\tan 2nx
1i think i made a mistake answer must be
solution
conider
(1+ei2x)n= nC0cos0 +nC1cos2 +nC2cos4+.....nCncos2n+i( nC0sin0 +nC1sin2 +nC2sin4+.....nCnsin2n)
Im((1+ei2x)n)/Re((1+ei2x)n)= answer