1i dunno.....just had this wierd idea....!!!
:-)
i think its of no use......
Give another method to find the no. of solutions (other than the method where bino. thm is used)
x+y+z = 24 , x,y,z≥0 and are integers
-
UP 0 DOWN 0 0 13
13 Answers
1can we do it by considering it as equation of a plane
all points ling on the plane will satisfy this equation........
1
106I have another method but i dunno how to apply it for ques like x+y+z+4w = 24 (other than taking w=0,1,2 ... and then finding)
106its a bit difficult, found it in our state board textbook, but here it is
Consider x+y+z = 5 where x,y,z ≥0
Then x+1,y+1,z+1 ≥1
=> l+m+n = 8 (where l,m,n are x+1,y+1,z+1) and l,m,n ≥1
This is the same as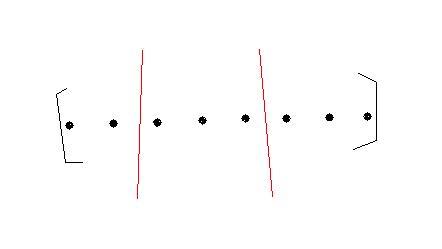
putting 2 sticks in the 7 gaps so as to divide the 8 dots into three groups which is 7C2
Same method can be applied for x+y+z+w = 30
also when there are restrictions on x,y,z ... (lower limits are fixed)
But i dont know how to use this if upper limits on x,y,z are given also of the form x+y+4z = 24 (except by fixing different values of z)
1i dunno...
maybe some expert can help.....
and wow u found this in ur state board book....gr8....never thought those books were any good.....
1for these sort of equation use this formula......
no.of solutions for the equation x1 +x2+x3 .....xr = C((n-1),(r-1)) if x1,x2,...are >0.
if they are ≥0 then C((n+r-1),(r-1))
so here use the second one since x,y,z≥0.
so we will get n=24 and r=3. so n+r-1=26 and r-1=2.
so answer is C(26,2)=(26*25/2)=650/2=325.
Like it.....
thank u...
1arey vishnuk5320
asish has already written not to use binomial....
:-)
1357The term n+r-1Cr is derived from here only
we have x+y+z=5
some of the solutions are
0+2+3
1+1+3
2+3+0
or lets denote it by stars
|**|***
*|*|***
**|***|
So basically you have to put 5 stars in 7 places
which can be done in 7C5 ways
106manish sir, i understud that. but i wanted to know how to do this question using the above method. like
x+y+z+4w=24
other than fixing different different values of w and solving separately
62Asish.. I dont know of a method to do the same...
What you could rather do is find the summation for each w
i mean x+y+z = 24 - 4w
and then the no of wa;ys will be 26-4wC2 for each w..
so take the summation over values of w of the above expression...
106but then using binomial doesnt require doing so much (although in the end you pretty much end up doing the same thing)
but what about this one?
x+y+z=16, 0≤x,y,z≤8 and x,y,z are integers?