2112[(a-b)2+(b-c)2+(c-a)2]=0
so (a-b)2+(b-c)2+(c-a)2=0
This is possible only when a=b=c
if, a2 + b2 + c2 = ab + bc + ac then find the relation between a,b and c for real values of a,b and c.
sitter question no doubt...
-
UP 0 DOWN 0 0 5
5 Answers
21
36Oops... sorry... then try this...
Find each sides of the triangle by pure geometry....!!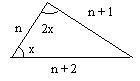
36sinc, LA = 2 LB
therefore, a^2 = b (b + c)
=> (n + 2)^2 = (n + 1)(n + 1 + n)
=> n^2 + 4n + 4 = 2n^2 + n + 2n + 1
=> n^2 - n - 3 = 0
now, find n... done :O