gif is floor function..means u pull down the sumthng.:D i mean dat 6.76 becomes 6.u pull it back.here is a graph check dis one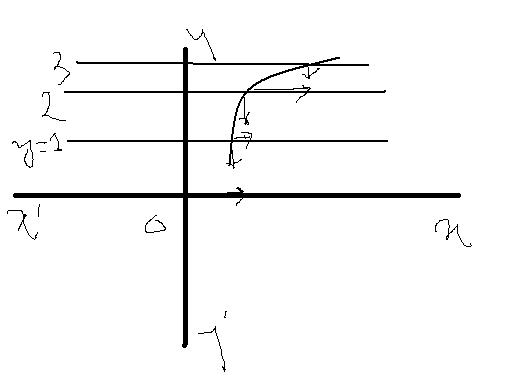 .
.
now take a value 1.76.since its hanging in air therefore it falls down on the floor i.e. 1.same case wid 1.99 or 1.23.but whn it cums to 2.0 its hanging by holdin 2 i.e. the roof .so it will not fall down.thus the gif of 2.0 is 2.
every now n then in calculus we encounter this function........moreover surprisingly while solving problems we come across a few properties which r usually not given under standard list given in books.........so i request all to send all the propeties they know of GIF in this thread so that we get all of them at a place in an exhaustive form
-
UP 0 DOWN 0 2 14

14 Answers
hey for greatest integer there is a page in ML khanna which lists some very useful formula for greatest integer :)
i kno dis falling falling part is sumwat pagal pagal type but dis is a gud way of understanding.n sorry for d bad handwriting :P
always remember that in GIF gravity acts downward n in least integer it acts upward.....nishant bhaiya's quote...:P:D
theorem???donno [3]
[-x] = -[x] - 1 , for x = noninteger
seee take an example like - 2.3 ,
and u will knowingly/unknowingly calculate wid d same eqn as above given
-2.3 becomes 3 right????? 2.3 becomes 2 if we take x= 2.3 nwe get -1 yeah ur right......
kalyan,[-2.3] becomes = -3.
[x]=greatest integer not greater than x(maybe equal to x).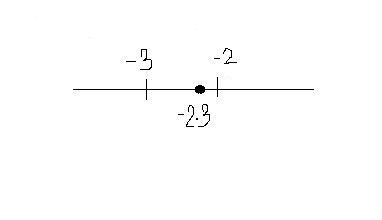
obviously -3 is the greatest integer not greater than -2.3.
ooppppsss my misstake.imissd out the minus........:P
A bunch of properties for y = [x] which I learnt in FIITJEE -:
P1 > [f(x)] = I (integer) where I <= f(x) < I+1
P2 > [[x]] = [x]
P3 > [x + I] = [x] + I where I is integer.
P4 > [a + [b + [c + [d]]]] = [a] + [ b ] + [c] + [d] for four reals a b c d.
P5 > [x] + [-x] = -1 if x is not integer, 0 if x is integer
Reasoning for P5 :
Let x = I + f where f is fraction and I is integer.
[x] + [-x] = [I + f] + [-(I + f)]
= [f] + [-f] which is always -1, if f is not 0. (try it and see)
P6 > [x + y] = [x] + [y], if 0<={x} + {y}<1
and [x + y] = [x] + [y] +1, if 1 <= {x} + {y} < 2
P7 > [x] > I implies x>= I+1
P8> [x] < I implies x < I
P9 > [x] <= I implies x < I+1