this inequality i think should be for n where n is an integer as n= 0.5 does not satisfy the inequality also please someone help me proceed. i'm getting stuck at this point. if we disprove the last inequality we are done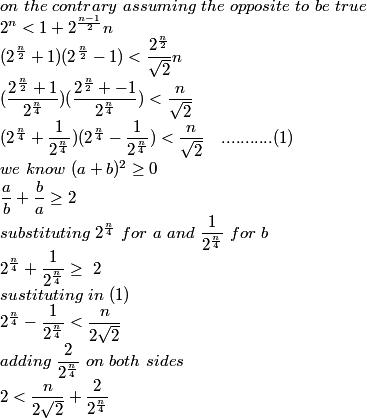
18 Answers
ok.. rahul.. it will be great if u could find something in that direction :)
1+2+22+... 2n-1 > (2n.(n-1)/2)1/n
n
take the AM GM for 1, 2, 22, 23.... 2n-1
note that the LHS above is =2n-1
Hence the proof of ur question....
from where u got the second eqn
(1+2+22+....+2n-1)/n > (2n.(n-1)/2)1/n
Nishant bhaiya im thinking of another approach.
if on the contrary we assume the opposite to be true
2n>1+2(n-1) / 2n
(2n/2+1)(2n/2-1) < 2(n-1)/2n
solving further we get 1 < n/√2 + 1/2n
thus if we disprove this equation we are done. so i'm working on it
2n ≥ 1 + n 2(n-1)/2
1+2+22+... 2n-1 > (2n.(n-1)/2)1/n
n
now thsi si obvious :)
at least type the question properly baba. you have written n 2(n-1)/2. you can cancel 2 in the num and denom as 2≠0. Thereafter 2n≥1+n(n-1) which is not true for n>2
Ok now u've changed it
buddy just try to prove it thru AM and GM inequality....
the same was told to me......
the inequality looks wrong to me. Were you trying to say 2n or something like that?