i think it would be better to use integration .
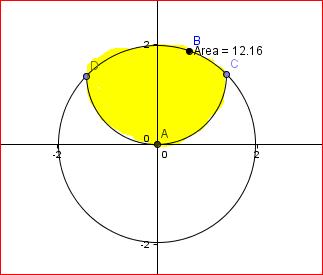
construct two eqns. of circles with radius 2 such that they pass through each other's centers.
eg . x2+y2=4 and (x-2)2+y2=4.
find their point of intersection.
integrate each one with proper limits.
6 Answers
A far far far better method is pure geometry..
A bit of trigo
Hint: Area of 2 secants :)
@Aditya. Yes I have done that. But that is troublesome (especially if you don't have time)
@Nishant Sir, Yes Sir! I was wondering for the same too. I'll try to scratch my head hard,to see if something comes.
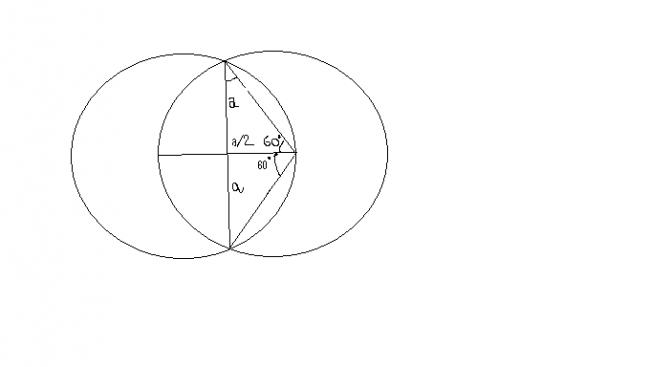
It can be easily done after this by finding the area of the two secants.
2(\frac{\pi r^{2}}{3} +\frac{1}{2}r^{2}sin120')
r=2
The points of intersection at (-sqrt(3), 1) and (sqrt(3), 1)
the length of the common chord is therefore 2*sqrt(3)
using Pythagoras theorem, the perpendicular distance from the center to the chord = 1
area of triangle ADC = 1/2 * 2*sqrt(3) * 1 = sqrt(3)
area of sector ADC = 1/6 * pi * r^2 = 0.67 *pi
area of the shaded area = 2* (0.67*pi - sqrt(3)) = 0.74 units (using symmetry)