In how many ways can one fill an n x n matrix with ±1 so that the product of the entries in each row and each column equals 1?
-
UP 0 DOWN 0 0 18

18 Answers
another method:
you can fill the elements a_{i,j} for i < n and j < n arbitrarily
then the elements a_{i,n} and a_{n,j} are determined
the only thing you have to check is that the a_{n,n} value comes out the same
what are u saying bhargav sol in #11 is already short and clear only
pls brief upon this finite fields ?
write 0 and 1 instead of -1 and 1
then we want the SUM of each row or column to be odd
consider this all in the field with 2 elements (so odd = 1 and even = 0)
now further proceeding is very easy.and soln becomes very shorter
but for this u need basic knowledge of finite fields.
[2^(n-1)]* [2^(n-2)]*[2^(n-2)]*[2^(n-3)]*[2^(n-3)]......
=2(n-1)+2(n-2)+2(n-3)+... rite...
and that way it comes to the same thing rite? or am i making a very silly error (like 7-8 grade type of silly mistakes)?
what ever, i some how feel dat the logic sits rite (although i dont think i been able to explain it very well, as i felt too lazy)
cheers!!
dude, but isnit
(n-1)+2(n-2)+2(n-3)+2(n-4)...+2
=2[(n-1)+(n-2)+(n-3)+(n-4)....+1]-(n-1)
=n(n-1)-(n-1)
=(n-1)2
rite?
i mean der cud be an error, (as i am into the habbit of making many)
if ders any plz point out..
cheers!!
gordo
is ur approach right ??
2^(n-1)* 2^(n-2)*2^(n-2)*2^(n-3)*2^(n-3)......=2n(n-1)/2
≠2(n-1)2
is it 2(n-1)2?
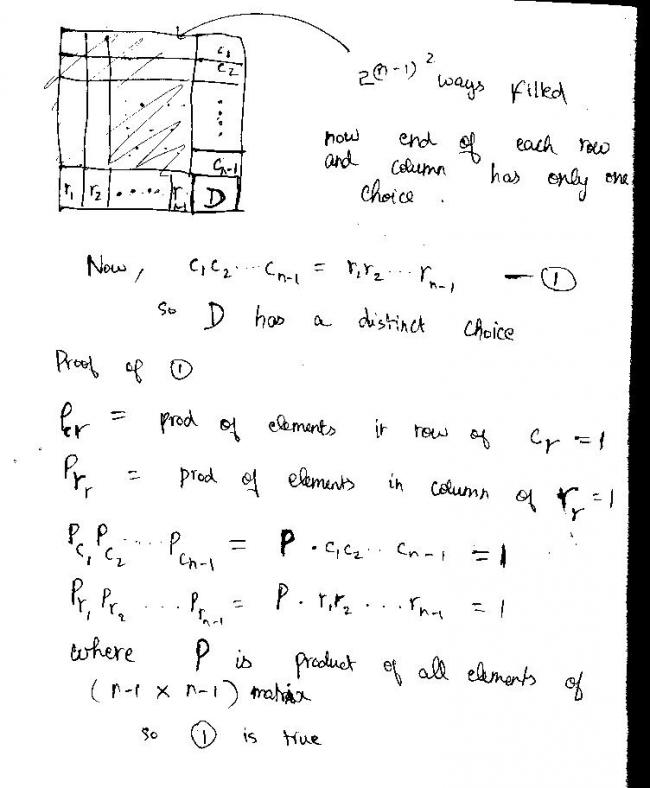
the first (n-1) elements of the first row can be filled in 2^(n-1) ways...elements of the first column(after the first and befor the last element) can be filled in 2^(n-2) ways...for each selection of elements in the 1st row and the first column, the last element has just 1 way of selecting itsself, such that the product remains +1...
similarly for the 2nd row and column together there are 2^(n-2)+(n-3) ways, for the third row and 3rd column put together there are 2^(n-2)+(n-3) ways, and so on and so forth intill der is jus 1 way (the last element)
so in a total der are
2^(n-1)* 2^(n-2)*2^(n-2)*2^(n-3)*2^(n-3)......
=2(n-1)2
cheers!!!
i din understand...can u make a bit clearer..
..as all the entries of the last row and last column are fixed so if we give +1 to the entry at the corner it may make the product of the last row +1...but the last column -1....we wont get the desired matrix then....
that wont be a problem abhirup
u can derive that prod of last row and last column without corner have same sign
if this case takes place....
if we give +1 to the entry at the corner it makes the product of the row +1...but the column -1
But what about the entry at the corner...that has to decide the sign of both the row and the column?
consider a
n-1Xn-1 matrix
ways of filling (±1) that is 2(n-1)2
now the remaining corners can be filled in only one way to make it into a nXn matrix so that product is 1 along rows and columns