A simple combi problem which suppossedly has multiple answers ?
Find the number of ways of arranging 5 distingushable balls into 3 distinguishable (differnet) boexes such that each contains at least one ball.
My logic (it looks like flawless)
First let us ensure that all 3 boxes get thei balls and then we can think about the rest two
so let us choose say 1st box so 5 ways of putting a ball for 2 -4 and similarly for 3-3 ways
thereofre there are 60 ways now of the remaining two balls both can go in any of the three containers so total=60*3*3 540 whats the right answer?? guys
1if i can calculate properly ur answers coming 300?
in tmh answer -120 ml khanna (the old one )-150 my answer is dammn sure right ;)
49sorry i did somethng wrng..
hadbari me gadbari! :P
it is:
(5C1.4C1.3C3+5C1.4C2.2C2).3!2!
you are overcounting some cases! check out carefully..!
21let me name the boxes as x,y and z......
so the no. of balls contained in x+y+z=5
and now x≥1 y≥1 and z≥1
\Rightarrow x-1≥0 y-1≥0 and z-1≥0
let x-1=a,y-1=b and z-1=c
so,
a≥0, b≥0 and c≥0
so, a+1+b+1+c+1=5
\Rightarrow a+b+c=3
so the possible values is 5C2............
1well acc to my calcuations i am not overcounting
we can rephrase my working in two parts as number of ways of distributing 3 balls out of 5 in 3 containers such that each contians ONLY 1 the answer i s
5C2* 3! (there is no overcounting in this case is there?)
iTHEN part 2 is we have two balls left the 1st ball can go in any of the 3 container .(therefore 3 ways and the second ball too in any of the 3 ways) (can anyone find any overcounting here
21how it comes let me show you.....................
there are 5 "identical" balls and 2 bars ........and we have to partition the balls......like this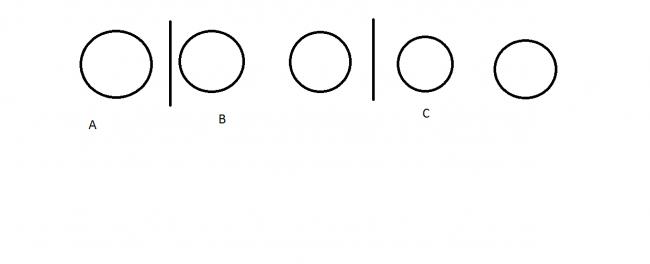
....... the A,B and C partitions give the value of a,b and c respectively.................now the no. of ways to put this 5+2=7 objects is
\frac{7!}{5!2!}=7C2..............got it?because there are 7 objects and two idebtical bars and 5 identical balls..........
now let there be n balls and r bars...............
so no. of partitions=r-1
the formula is
\frac{(n+r-1)!}{(r-1)!n!}=(n+r-1)c(r-1)
so put it in your q..............and you get the ans. in my process.................
30No. of ways to distribute 5 balls (different) among 3 different boxes without any restrictions- 35
Now, the invalid cases here are when 2 out of 3 boxes are empty and 1 out of 3 boxes are empty. Lets count them.
Case 1 (2 out of the 3 boxes are empty):
No. of ways = 3, because for 2 boxes to be empty all 5 balls will be in one box, and that one box can be selected in 3 ways.
Case 2 (1 out of the 3 boxes are empty):
No. of ways = (25 - 2)*3, because the one box that'll be empty can be selected in 3 ways.
So, now coming back to the original question,
No. of ways to distribute the balls such that each box has atleast 1 ball = 35 - 3 - 3(25 - 2) = 150
Whats the final answer?
1
3 1 1 5C3*2C1*1C1=20
2 2 1 5C2*3C2*1C1=30
1 3 1 5C1*4C3*1C1=20
1 2 2 5C1*4C2*2C2=30
1 1 3 5C1*4C1*3C3=20
2 1 2 5C2*3C1*2C2=30
=150
49vaibhav's answer is same as mine! [1] nice job!
@Ashish: masst solution! [1]
49okay varun: Share ur mistake with the for fellow students to get a view into the world of "what not to do in perm-comb" ;)
do it soon.. [1]
1My solution Let us assume
CASE 1
one box has three balls
therefore 3C1 (ways to choose which one)
3c1*5c3*2c1
Case 2
two boxes have two balls
3c2*5c2*3c2
add it to get 150
My mistake was basically this i was trying to check whether i actually knew when to use the fundamental principle sof counting so i tried to do that and never checked abut overocunting but whatever i am gonna start a combinatorics thread for everyone something like artofproblemsolving
so wait for my thread