71Find all z in form of a+ib satisfying the relation below:
(3z-1)4 + (z-2)4 = 0
Let n be a positive Integer. 0<\theta _{i}<90, such that
cos^{2}\theta _{1}+cos^{2}\theta _{2}+cos^{2}\theta _{3}+.....+cos^{2}\theta _{n} = 1
PROVE THAT:
tan \theta _{1}+tan \theta _{2}+tan \theta _{3}+...+tan \theta _{n} \geq (n-1)(cot\theta _{1}+cot\theta _{2}+....cot\theta _{n})
-
UP 0 DOWN 0 0 13
13 Answers
71
1seems some trick has to be applied in the second question
or else we have to solve the quartic equation
21if we put tan∂ = A the inequality becomes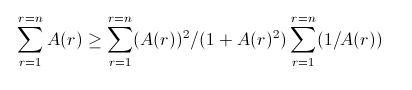 
where we have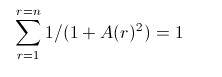 
i tried to prove the inequality by chebychefs but it did not go well.....
pls somebody try this one...
21we have
tan ∂i = sin∂1cos ∂1 = √1-cos2∂1cos∂1 = √cos2∂1+ cos2∂2 +.....+cos2∂i-1 + cos2∂i+1+.....+ cos2∂n
cos∂1
from m-th power inequality √x2+y2 √2≥x+y2
so tan∂i ≥ cos∂1+ .....+ cos∂i-1+ cos∂i+1+...+ cos∂ncos∂1√n-1
summing the inequality for i from 1 to n we get
tan∂1+...+ tan∂n ≥ 1√n-1\sum_{}^{}{1\leq i,j\leq n,i\neq j}ajai
because each ratios ajai appear only once
on the other hand
cot∂i = cos∂isin∂i= cos∂i√cos2∂1+ cos2∂2 +.....+cos2∂i-1 + cos2∂i+1+.....+ cos2∂n
again we have from m-th power inequality
√x2+y2 √2≥21/x + 1/y
so cot∂i ≤ cos∂i (1cos∂1 + ....+1cos∂i-1+ 1cos∂i+1+...+ 1cos∂n)(n-1)√n-1
again after summing up we get
cot∂1+ ...+ cot∂n ≤\sum_{}^{}{1\leq i,j\leq n,i\neq j}ajai
(n-1)32
combining above two inequality
we get
√(n-1) (tan∂1 +....+ tan∂2) ≥ \sum_{}^{}{1\leq i,j\leq n,i\neq j}ajai ≥ (n-1)32(cot∂1 +....+ cot∂n)
so (tan∂1 +....+ tan∂n) ≥(n-1)(cot∂1+......+ cot∂n)
21one of my teacher really helped me by giving valuable hint on which inequality to use here.
71Where can I get more details/applications of this Inequality.
@Subho BTW, Did u appear for this year's RMO?
21i did, didn qualify ,will give a best attempt this time
"where can i get......"
please specify..
71I meant if there is any online source/link available or have to consult teacher.. (Although they won't tell)
I was having a look through my problems collections once and found this.. They are collected from various sources.. Like say wherever I see a good problem I write it down and get it solved at appropriate time..
21we know AM of mth power ≥ m-th power of AM
so x2 + y2/2 ≥ [( x+y)/2 ]2
taking square root we get √x2+y2√2≥x+y2
from AM≥ HM
x+y2≥21/x+1/y
so √x2+y2√2 ≥ 21/x+1/y
