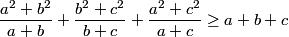1
1Just substitute
a=1+A
b=1+B
c=1+C
d=1+D
AS they all are >1
: = A,B,C,D >0
then we need to prove
8((1+A)(1+B)(1+C)(1+D)+1)>(A+2)(B+2)(C+2)(D+2)
=>
8(ABCD+ΣABC+ΣAB+ΣA+2)>16((A/2)(B/2)(C/2)(D/2)+ΣABC/8
+(ΣAB/4)+ΣA/2+1)
simplifying ,
8ABCD+8ΣABC+8ΣAB+8ΣA+16>ABCD+2ΣABC+4ΣAB+8ΣA+16
which can be clearly seen
 341
341WLOG aa \ge b \ge c \ge d
The sequences (1,1) and (a,b) are similarly ordered.
So, from Chebyshev's Inequality, we have 2(1+ab) >=(1+a)(1+b)
Similarly, we get 2(1+cd) >= (1+c)(1+d)
Again, the sequences (1,1) and (ab,cd) are similarly sorted.
So, 2(1+abcd) >= (1+ab)(1+cd)
Hence 8(1+abcd) >= 2(1+ab) 2(1+cd) >= (1+a)(1+b)(1+c)(1+d)
 1
1@prophet sir
what u've used---- Chebyshev's is it mandatory to know it for jee
 341
341I dont think so. I havent seen any real use of inequalities in JEE beyond AM-GM.
The standard ones in Integrals (Riemann sums), and m(b-a) <= I <= M(b-a) those are used at times
 1
1nice solution prophet sir.
a,b,c are positive real numbers. prove
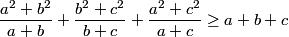
 24
24knowing Chebychef's,Cauchy-Schwarz,Jensons....helps a lot.....[1]
 1
1hey minister eureka can u post an article over Chebychef's,Cauchy-Schwarz,Jensons
 106
106please post in a new thread...
 1
1well we see that
a2+b2/a+b >(a+b)/2 as
It reduces to
a2+b2>2ab which is true as (a-b)2>0
so applying it on the other two terms we get
>= (a+b)/2 +(b+c)/2 + (c+a)/2=a+b+c