1why nobody is replying
Locus of z if
3π/4 when !z! ≤ !z-2!
arg [z–(1 + i)] = and is ?
-Ï€/4 when !z! > !z-2!
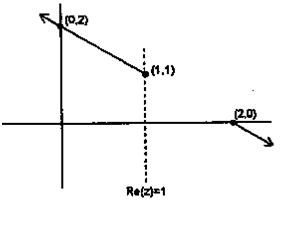
(A) Straight lines passing through (2, 0)
(B) Straight lines passing through (2, 0), (1, 1)
(C) A line segment
(D) A set of two rays
-
UP 0 DOWN 0 0 12
12 Answers
1Can u please post the question again ?
The statements seem to be quite jumbled up.....
1Z ka locus batana h condition is given arg. of [Z(1 + i)] is equal to this and this
39Let z = x + iy.
(x + iy)(1 + i) = x + ix + iy - y
= x - y + (x + y)i
The argument of this would be tan-1((x + y)/(x - y)).
I'll solve the rest of this when I get back from walk...others can try after applying the modulus condition to x + iy.
|z| = √x² + y²
|z - 2| = √(x - 2)² + y²
Use the above two equations as your conditions(or region equations) to apply on the argument = 3pi/4 or -pi/4. You'll get your answer.
Square both sides of inequality to make it easier.
Ok back now...first let's find the region conditions from the inequalities.
The first region is |z| ≤ |z - 2|
=> x² + y² ≤ x² + y² + 4 - 2x
=> 2x - 4 ≤ 0
=> x ≤ 2
Similarly the second region is x > 2.
So our expression arg[z(1 + i)] = 3pi/4 if x ≤ 2
and -pi/4 if x > 2.
Now for x ≤ 2,
tan-1[x + yx - y] = 3pi/4
=> x + y = y - x as tan(3pi/4) = -1.
=> x = 0 or the Y-axis.
For x > 2,
tan-1[x + yx - y] = -pi/4
Which is again x = 0.
So for all regions, x = 0 or the Y-axis is the locus.
I guess the answer is (C) then?
39How is the ans D? I was sort of thinking ki x = 0 aur y = 0 aayega...so that would be a set of rays originating from x = 2. But calculate karne par toh aisa nahi aa raha!
Okay...is it like...we have x = 0 in the expression z = x + iy. So z = iy or purely imaginary for all regions, meaning it is a set of rays in the Argand plane?
