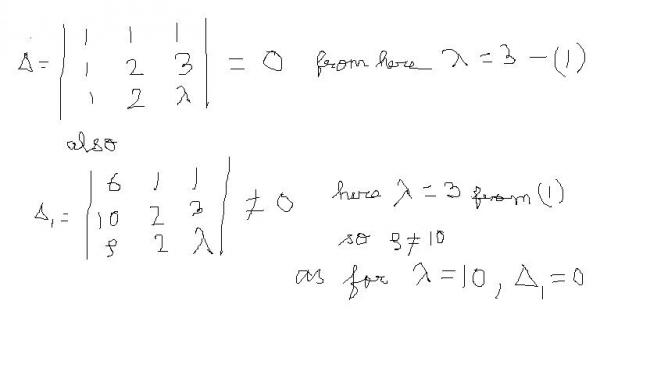Matrices and determinants

Got the second one... please try the other two.

I haven't encountered questions which says "expressed as linear polynomial''....what does it mean?
finding A³.. A² also doesn't seem to help.

\begin{bmatrix} 1 & 4\\ 2 &3 \end{bmatrix}

now finding characteristic equation by cayley hamilton

we get equation as

A^2 - 4A - 5I = 0 ---- 1

from d given equation we have

A^5 - 4A^4 - 7A^3 + 11A^2 - A - 10 I

which can be written as

A^5 - 4A^4 - 5A^3- 2A^3 + 11A^2 - A - 10 I

now combining first three terms

(A^5 - 4A^4 - 5A^3 )- 2A^3 + 11A^2 - A - 10 I

A^3(A^2 - 4A - 5I )- 2A^3 + 11A^2 - A - 10 I

BUT THE EXPRESSION IN bracket is 0 ( from ---1 )

equation reduces to

A^3(0 )- 2A^3 + 11A^2 - A - 10 I

this equation can be written as

- 2A^3 + 8A^2 + 3A^2+ 10A - 10 I - ( 11 A)

REARRANGING

( - 2A^3 + 8A^2 + 10A)+ 3A^2 - 10 I - ( 11 A)

THIS EQUATION REDUCES too

- 2A( A^2 -4A -5I)+ 3A^2 - 10 I - ( 11 A)

again expression in bracket is 0 ( from ---1 )

equation reduces too

3A^2 - 10 I - ( 11 A)

which can be written as
3A^2 - 12A -15 I + ( A + 5I)

3 [ A^2 - 4A -5 I ] + ( A + 5I)

EXPRESSIon is square bracket is 0

hence ans is

option a)

Q1.

[ C₁ → C₁ + C₂ + C₃ ]
\begin{vmatrix} 1+a^{2}x+x+b^{2}x+x+c^{2}x & (1+b^{2})x & (1+c^{2})x\\ x+a^{2}x+1+b^{2}x+x+c^{2}x& 1+b^{2}x &(1+c^{2}) x\\ x+a^{2}x+x+b^{2}x+1+c^{2}x&(1+b^{2})x & 1+c^{2}x \end{vmatrix}

\begin{vmatrix} 1+2x+(a^{2}+b^{2}+c^{2})x & (1+b^{2})x & (1+c^{2})x\\ 1+2x+(a^{2}+b^{2}+c^{2})x& 1+b^{2}x &(1+c^{2}) x\\ 1+2x+(a^{2}+b^{2}+c^{2})x&(1+b^{2})x & 1+c^{2}x \end{vmatrix}

=\begin{vmatrix} 1 & (1+b^{2})x & (1+c^{2})x\\ 1& 1+b^{2}x &(1+c^{2}) x\\ 1&(1+b^{2})x & 1+c^{2}x \end{vmatrix}

=\begin{vmatrix} 1 & (1+b^{2})x & (1+c^{2})x\\ 0& 1+b^{2}x-x-b^{2}x &(1+c^{2}) x-x-c^{2}x\\ 0&(1+b^{2})x-x-b^{2}x & 1+c^{2}x-x-c^{2}x \end{vmatrix}

=\begin{vmatrix} 1 & (1+b^{2})x & (1+c^{2})x\\ 0& 1-x &0\\ 0&0 & 1-x \end{vmatrix}

=\begin{vmatrix} 1-x &0 \\ 0& 1-x \end{vmatrix}

= ( 1 - x )²
= x² + 1 - 2x

hence degree is 2

for 2,use cramers rule.
for the equations to have no solution,
Δ=0(where Δ is the determinant of the cofficients of x,y,z)
Δ₁≠0(if all of them are 0 there will be infinite solutions)