min Value

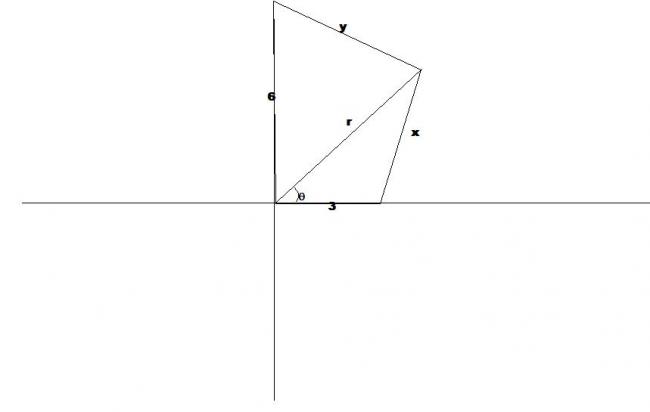
it represents any any random complex number with |z|=r , x=|z-3|,y=|z-6i|
now applying cosine law for the two triangles , wee get
x²=r²+9-6rcosθ and
y²=r²+36-12rsinθ
adding both of them and adding r² both sides
|z|²+|z-3|²+|z-6i|²=3(r²+15-2r(cosθ+2sinθ))
this is quadratic in r and te minimum value of any quadratic with a>0 is -D4a
hence
f(min)=15-(cosθ+2sinθ)²
this expressions min value is when (cosθ+2sinθ)² attains max =5
hence min value is ( 15-5 ) *3 =30

the given represents the sum of the sqaures of the distances of a point z from vertices of the traingle having cordinates (0,0) (3,0) (0,6) and that z point is centriod of the triangle

In fact If you write z=x+iy you will notice that that the expression can be written as F(x) + G(y). We can separately minimise F and G and thus obtain the minimum value of the given expression.

That is how we see that the minimum is obtained when z is the centroid. (In fact i have seen this result in one of the X Class math guides!)