12 )
a graphical approach
graph of y =[x]*{x}
and graph of y=x
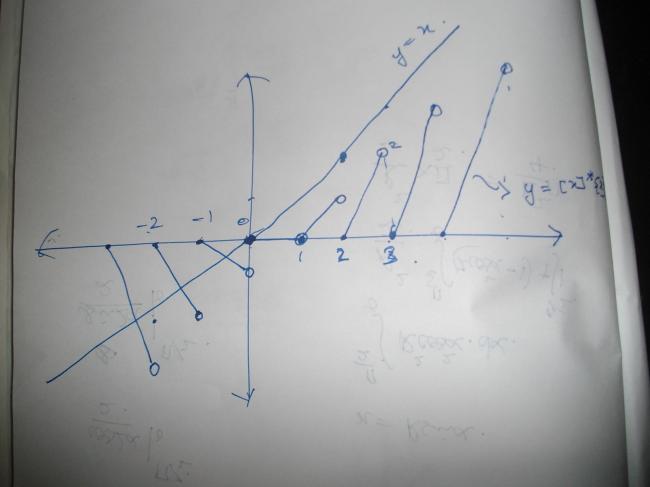
we can see infinite number of solution
(1) find value of x in | | | |x| - 2| - 2|- 2| = | | | |x| - 3| - 3|- 3|
where | x | denote Modulus function.
(2) find real solution of the equation [x]*{x} = x.
{ } = fractional part function.
[ ] = Integer part function.
-
UP 0 DOWN 0 0 2
2 Answers
1
12 > Given ,
x [ x ] - [ x ] 2 = x ...............using the fact { x } = x - [ x ]
or , [ x ] 2 = x [ x ] - x = x ( [ x ] - 1 ) = x . ( an integer ) .................. ( 1 )
Clearly , [ x ] 2 is an integer .
So , R . H . S of the said relation ( 1 ) must also be an integer , which must be a perfect square .
For that , x must be an integer , or x must be a proper fraction whose denominator must divide [ x ] - 1.
But if x is an integer , then [ x ] = x .
So , the given relation yields x = 0 as the only solution in integers .
But the other case yields infinite solutions .
