Ans i think is
3) no complex roots
edit
The equation A2/(x-a) + B2/(x-b) + C2/(x-c) + ..... + H2/(x-h) = k has
1) No real root
2) At most one real root
3) No complex root
4) At most two complex roots
-
UP 0 DOWN 0 0 8

8 Answers
DanTe^ ,sorry i made stupid mistake.
I am proving this for the equation A2/(x-a) + B2/(x-b) + C2/(x-c)+ D2/(x-d) = k (same arguments hold a,b,c,d,e,f,g,h )
Design a polynomial function f(x) = A2(x-a) B2(x-b)C2(x-c)D2(x-d)
Taking log and differentiating we can say f'(x)/f(x) = A2/(x-a) + B2/(x-b) + C2/(x-c)+ D2/(x-d)
So we have to solve f'(x)f(x) = k , or kf(x) - f'(x) = 0
Let P(x) = kf(x) - f'(x) ,Let k>0 (similar arguments hold for k<0)
From the graph of f(x)[drawn with help of Rolle's theorem] check the sign of p(x). from the figure given.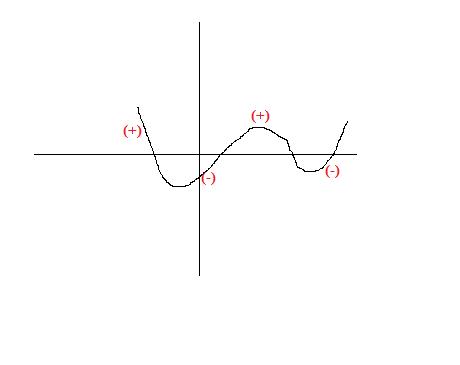
There is at least one root in between points of each sign change. Hence we clearly see 3 real roots of p(x). As p(x) is an polynomial equation with real co-efficients complex roots must occur in conjugate pairs. so there can't be a single complex root. so all roots are real.
(while checking the sign of p(x) , use the fact that when slope of tangent at any point is negative f'(x) at that point is negative)
I take it that A,B, ...,H, a,b,c...,k are all real
So, suppose z is a root, so is its conjugate
Hence
\frac{A^2}{z-a} + \frac{B^2}{z-b} +....+\frac{H^2}{z-h} =k
and
\frac{A^2}{\overline{z}-a} + \frac{B^2}{\overline{z}-b} +....+\frac{H^2}{\overline{z}-h} =k
Let z-\overline{z} = iR, R \in \mathbb{R}
Then subtracting and simplifying, we obtain
iR \left(\frac{A^2}{|z-a|^2} + \frac{B^2}{|z-b|^2} +....+\frac{H^2}{|z-h|^2} \right)=0
Since the bracketed term is positive, we must have R=0.
In other words roots are purely real
one more proof could be by cross multiplying...
We see that the polynomial we have is of n degree...
Moreover the original question has one root between xi and xi+1 this is simply done by using limits because the right limit at xi is +ve infinity and left limit at xi+1 is - infinity
Also by saying that the function is continuous in between the limits...
Hence the polynomial has atleast n-1 roots...
There cant be 1 single complex root..
Hence all roots are Real.
got it nishant bhaiya has used the asymptotes ,this gives the same resullt as that of shubodip