3 .
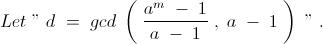
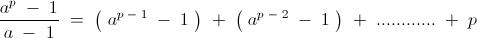
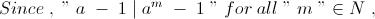
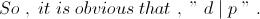
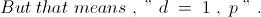
1)For n≥3 determine all real solutions of the system of n equations
x1+ x2+...+xn-1 = 1xn
............
x1+ x2+ ...+xi-1+ xi+1+...xn= 1xi
.......
x2+ ...+ xn-1+ xn = 1x1
2)Suppose P(x) is a polynomial with real coefficients such that for some positive real number c,d and for all natural number n , we have c|n|3≤|p(n)|≤d|n|3. Prove P(x) has a real root.
3)If p is a prime and a>1 is a natural number ,then show that gcd(a-1 , ap-1a-1) = 1 or p
4)Find all triples (x,y,p), where x and y are positive integers and p is a prime satisfying the equation x5+ x4+ 1 = py
5)Find positive integer (m,n) satisfying mn + n+1m= 4
6) http://www.targetiit.com/iit-jee-forum/posts/polynomials-19403.html
7)Prove for odd m , m(m-2)|2(m-1)! - 1
solution to problem 8. let x≥4 ,f(4+x) = f(4x) = f(2x+2x)= = f(4x2) = f(4x.x) = f(4x+x) = f(5x)= f(5+x)[4]
prob 8=# 9 (btw nokia '5233' is a phone that i had,its a prime)
infectious! :P
its good to see you guys are having fun doing math. I hope this enthusiasm is infectious.
BTW, which is the 8th prob?
Ricky i dont understand 6. explain how u got m|n , m|n+1..i guess u have n|m2
another solution: write this as (m-2n)2 = n(3n-1). gcd(n,3n-1) = 1. 3n-1 is a perfect square. contradiction! (source: AOPS)
The 8-th one is tricky!!
Prophet sir, hope u don't kill me if i say this thread was made by ricky and me for fun and to create some action......[3] For q (2) i spent sometime to see whether i can use IVT. Otherwise this is plain ...this was from ISI Bmath paper 2008.
When i looked over the solution again i realized that you dont need that
x≡2 mod p
One of the factors divides the other is all that you need.
x^5+x^4+1 = (x^2+x+1)(x^3-x+1)=p^y
Now, we clear up the case when one of the factors equals 1.
For natural numbers x, we have x^2+x+1 \ge 3 so we only need to check the other factor and we see that equality occurs when x=1.
Verifying, we see that we have (1,1,3) as one solution.
Now, if both the products are greater than 1, we must have
x^2+x+1 = p^{n_1}; x^3-x+1 = p^{n_2} with n_1+n_2=y
So p divides both numbers so that it also divides
(x-1)(x^2+x+1)-(x^3-x+1)=x-2
i.e. x \equiv 2 \pmod p
Now,
x^2+x+1 \equiv 2^2+2+1 \equiv 7 \equiv 0 \pmod p \Rightarrow p=7
So, we have
x^2+x+1 = 7^{n_1}; x^3-x+1=7^{n_2}
That means x^2+x+1 |x^3-x+1 \Rightarrow x^2+x+1|x-2
Since x^2+x+1 > x-2 this is possible iff x=2
Verifying we see that (2,2,7) is also a solution
Thus the only solution sets are (1,1,3) and (2,2,7)
2) is quite trivial as you only need to prove that P(x) is a cubic
Proof: WLOG the leading coefficient of P(x) is positive. Let P(x) be of degree k
For large enough n, we have P(n)≥0 and so we can drop the mod.
Then the inequality becomes
cn^3 \le a_n n^k+a_{n-1}n^{k-1}+...+a_0 \le dn^3
or
c \le a_n n^{k-3}+a_{n-1}n^{k-4}+...+\frac{a_0}{n^3} \le d
Let us see what happens when n \rightarrow \infty
If k>3, we get d \ge \infty which is absurd
Again if k<3, we get c \le 0, but we are given c>0
Hence k=3.
But we know that any polynomial of odd degree has at least one real root and so we are done
7)
First note that m and m-2 are relatively prime as otherwise their gcd would divide m - (m-2) = 2, which would mean gcd =2 which is absurd as m is odd.
So it suffices to separately prove divisibility by m and m-2
Now by Euler Totient theorem we have
2^{\phi(m)} \equiv 1 \pmod m
Since\phi(m) \le m-1, we have \phi(m)| (m-1)!
Hence it follows that 2^{(m-1)!} \equiv 1 \pmod m
By a similar argument 2^{(m-1)!} \equiv 1 \pmod {(m-2)}
m and m-2 being relatively prime we have
2^{(m-1)!} \equiv 1 \pmod {m(m-2)}
thus proving the assertion
6 . Write the given equation in the form -
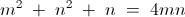
Taking each side " modulo ' n ' " and " modulo ' m ' " , we arrive at -
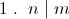
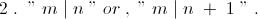
It is easy to see that these set of conditions are never fulfilled by positive integers .
since if x1 *x2 =1 , then comparing similar results we have x1=x2 =....... = xn =±1
which does not satisfy the reqd. condition
and of course x will have ± 1/√(n-1)
x= ± 1√n-1
8)Find all function f:\mathbb{N}\to\mathbb{N} satisfying f(x+y)=f(xy) for all x,y\geq4 and f(5233) = 279
adding all lhs and rhs ,
(n-1)\sum{x_{i}} = \sum{\frac{1}{x_{i}}} ... (i)
using eq. (i) in the first eqn ,
(n-1)(x_{1} +1/x_{1}) = \sum{\frac{1}{x_{i}}}
similarly ,
(n-1)(x_{2} +1/x_{2}) = \sum{\frac{1}{x_{i}}}
similarly for others,
dividing these eqns ,
we have ,
(x_{2} +1/x_{2}) = (x_{1} +1/x_{1})
or ,x_{1} =x_{2} (since x1 * x2 =1 is not possible )
hence, = x (say)
replacing in any eqn ,
(n-1).x = 1/x
or, x = \frac{1}{\sqrt{n-1}}
A try
Let us consider a case
x1=x2=x
x1=x3 =x
.
.
.
x1=1xi ≡xi=1x
.
.
.
From one of the conditions
kx+lx=0
no real solutions for x
??
so only possible solution is
x1=x2=x3=x4.....xn=1√n-1
is it right ?
For Nishant bhaiya's hint
x1 =x2
or
x1=1x2
I think , the answer is x1=x2...=xn=1√n-1
Not sure
That one one is trying these....
Let me give some hints to the 1st question...
If x+1/x = y+1/y then what is the relation between x and y?