33deleted that...
3 can be written as
1+1+1
2+1
1+2
3
(4 ways..)
In how many ways n can be written..
_________________
I think I posted this one earlier... in some post...(Nisahnt bhaiya gave the answer but not the method...that time...(sayad...jaha tak mujhe yaad hai))
(But later I solved it....and din' found that thread to post the solution so am starting a new thread.. :P)
so others may try this one....
-
UP 0 DOWN 0 0 20
20 Answers
11i got a different method
n=1+1+.......n times
these ones can be grouped when you take all the ones together one way corresponding to nC0
so consider nC0+nC1+.....+nCn
but nC0 and nCn correspond to the same because in both cases we take all the 1s together
similar logic for all the other terms show that the expression has to be divided by two
so 2n-1
this time am i rite with my logic bhaiyya??
and bhaiyya the writing is on the screen[3]
62I mean if he wants to write
5=2+2+1
how will subash's method work!
21SIR can u xplain wat dus this mean ?
Then ho wdo you cover the cases by your method of having
2 groups of 2?
62Then ho wdo you cover the cases by your method of having
2 groups of 2?
11it can also be given by nC0 because choosing no ones is equal to taking all the ones
nC2 is grouping 2 ones together
that is writing is as 2+n-2
62I appreciate your way of thinking but
I did not understand the method clearly
:(
why divided by 2?
Why is no of ways to chose all the 1's = nC0?? it should be nCn
What does nC2 stand for?
62Subash the writing is on the wall!
Just refer to what priyam wrote!
33
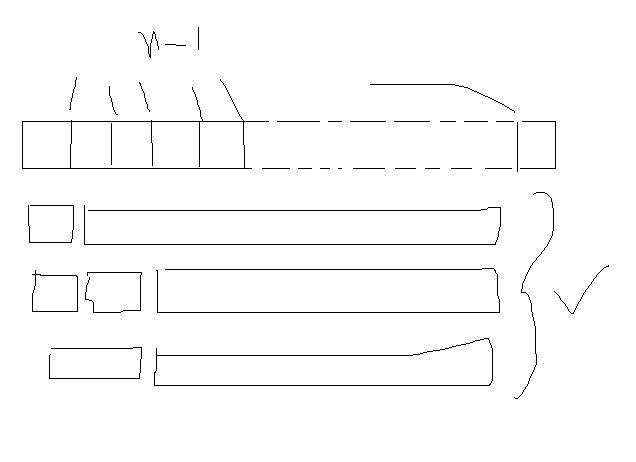
It is no of ways cutting the cake having n-1 slots...
2n-1
each slot has two option either to be cut or not...
no of slots = n-1
so 2n-1
1why is this not in "p n c" is there some diff trick involved...?...
looks so much like..
sum of no of solutions of
a = n
a+ b = n
a +b +c =n
.
.
.
a +b + c + .. ...+(char)(n+97)= n (ASCII :D)
now please dont argue that this will only make sense for n <=26 :D
