2n points are chosen on a circle. In how many ways can one join pairs of points by non-intersecting chords?
66There are 2n points, so how many many pairs do you think? However, the question does not ask about the number of pairs; rather the number of ways of ways of joining them so as to have non-intersecting chords.
39Well...I'm possibly nowhere near the answer but...
If we take n points on one half of the circumference and n points on the other(diametrically opposite), then we join them sort of like we see in a one-one function's Venn diagram.
There can only be one way of joining n points on one side to n points on the other so that the chords so formed can never intersect(i.e, parallel chords).
66But there are possibly more ways of taking the two halves of the circle itself.
39But...it's how we look at the circle isn't it? Otherwise there could be n number of ways to halve a circle..
66You didn't get the point. The points are distinct. May be they are labeled. For n = 3, that is, for 6 points the following five are the ways: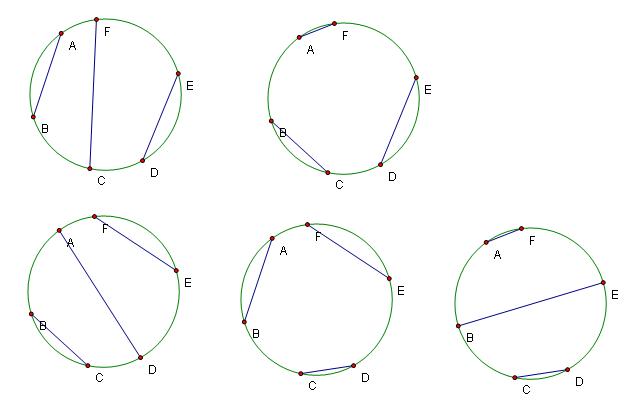
39Ah...then they don't intersect in the circle but do so outside...I get it now. I thought they shouldn't intersect at all!
341This puts me in the mind of a classic problem that asks in how many ways can we arrange n brackets in a balanced way (i.e. number of left brackets = no. of right brackets). And the answer lies in the Catalan numbers. So the number of ways must be Cn [ http://en.wikipedia.org/wiki/Catalan_number]
66Exactly. The required answer is the n-th Catalan number Cn = 1n+1 2nCn.