1[7][7][7][7][7][7][7]
A square of n units by n units is divided into n2 squares of 1 sq. unit each. find the number of ways in which 4 points ( out of (n+1)2 points) be selected so that they form the vertices of a square.
i was able to count the number of squares whose sides are horizontal and those whose sides are at 45° to horizaontal. please tell me how to count squares of this type..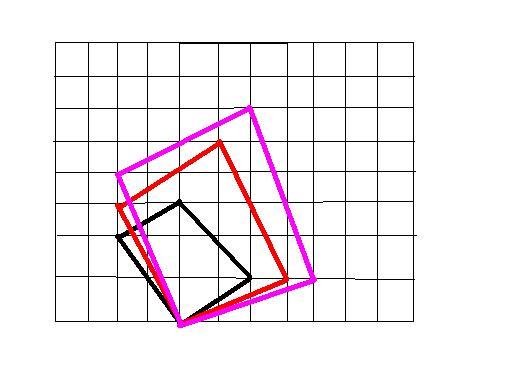
(they dont appear to be squares but they are if diagram is accurate)
also suggest any alternate method as i find this method cumbersome
-
UP 0 DOWN 0 2 4
4 Answers
9method :
Observe that each square of side r can have exactly r-1 diff squares inscribed inside it .
So evidently in the region occupied by a rXr sqr , r sqrs are present .
we know no of rXr regions = (n+1-r)2
so ans is
Σ(n+1-r)2 .r which can be calculated