1yeah...i drew that only..
i hve two ways either I choose 5!+4.4! or the subtraction of the two...
look at dis
do tell wat is correct....
pls ans dis ques
how many five digits numbers can be formed using the digits 0,1,2,3,4,5 so that the numbers are divisible by 6..??
-
UP 0 DOWN 0 0 25
25 Answers
11yeah...didnt thought dat way...
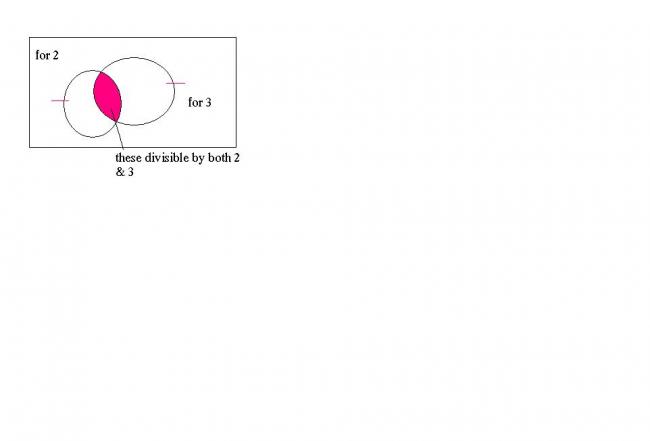
this was just da basic thing i should hve thought... combining divisibility of 2 & 3...
thnx
62arrey shreya there is nothing new in this..
it is like the intersection of both
divisibility by 2: last digit 2
divisibility by 3: sum of digits divisible by 3...
so the intersection of numbers gives those that are divisible by 6: hence they have to follow both these rules...
BUt the thing is that this wont work in ur method!
1okay...so i would hve to abandon my method...
actually i didnt knew dat for divisibility by 6 we should go for "last digit even and sum of nos divisible by 3"....
kk will go by dis..
n
thankyou!!!
62Repeating what i said earlier...
0,1,2,3,4,5
divisibility by 6 needs that the last digit is even and that the sum of digits is divisible by 3..
so the possiblities of divisibility by by 3 is only by leaving out 0 or 3
here in the following case.. i am filling the last digit with either 0 or 2 or 4 ... depending on the case....
Case 1: we leave out 0, the number of ways is : 2.4!
Case 2.1: we leave out 3, and 0 is the last digit, the number of ways is 4!
Case 2.2: we leave out 3 and 0 is not the last digit, the number of ways is 2.3.3!
so the sum is
4!.3+3!.6 = 3!.18= 108
1okay..i accept dat..but den how do u found A∩B?????? [i dont hve x and y...i only hve complete A and B]
62i will give u another example..
what is the number of numbers divisible by 5 in the numbers 1-100
and the number of numbers divisible by 2 in 1-100
first one is 20
2nd one is 50
what is the intersection.. *numbers divisible by 10 (right?)
so it is 100/10 = 10
but the difference will give 30.
62no this is now wrong...
what i am saying is that the way you are finding the intersection is wrong..
the intersection is not the difference of these two numbers...
A∩B ≠A-B
1for nos divisible by 2
fix 0 at the last place then total ways are 5!
fix 2 at the last place u get 4.4!
fix 4 at the last place u get 4.4!
so total ways for nos divisible by 2 are 5!+2.4.4!
for nos divisible by 3
we hve 2 sets for dis
[1,2,3,4,5] and [0,1,2,4,5]
for Ist set total ways are 5!
for IInd set total ways are 4.4!
so total ways for nos divisible by 3 are 5!+4.4!
and, then, nos divisible by 6 will be the intersection of the two...
wat do u say??
is dis wrong????????
62hey shreya.. sorry for that... you just needed to press F5 and then submit...
Anyways...
i am here... and will try to explain to you...
1da site was temporarily disabled!!!!!!i would hve to type dat all again!!!!!!!! dont go away before telling me da solution
62did u understand my method shreya???
I think there is a mistake in what u have given...
I cant exactly understand how u got to the numbers that u did....
62(i think u also mean that we can use each digit only once?? I am solving using that assumption...)
0,1,2,3,4,5
divisibility by 6 needs that the last digit is even
and that the sum of digits is divisible by 6..
so only digit that cant be here is 3!!!
so we have to have 2. 4 or 0 as the last digit using the digits 0,1,2,4,5
Now can u solve it?
I went mad again.....
62
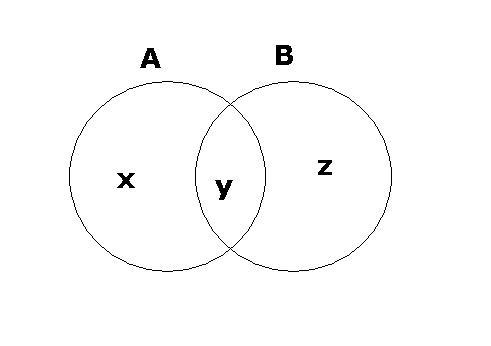
in this image... set A is the divisibles of 2
set B is the divisibles of 3
A=x+y is given by ur first term
B=y+z is given by ur second term...
we need to find y
but u have found A-B = x-z
62no shreya this is not the correct method...
think of it in terms of set theory...
draw a venn diagram...
1i lik calculated all da nos divisible by 2 from these digits ans was 5!+8.4!
total nos divisible by 3 were 5!+4.4!
now, i think that these two should be subtracted....
m not sure if i hve done it rite!!
62both of us are saying the same thing....
well the intersection is correct.. but how did u get the intersection?
it depends on how u got to the intersection... can i know ur method?
1pls tell me first wat is da divisibility criteria for 6 ..da one i mentioned or da one u r saying?????
62(i think u also mean that we can use each digit only once?? I am solving using that assumption...)
0,1,2,3,4,5
divisibility by 6 needs that the last digit is even
and that the sum of digits is divisible by 3..
so the possiblities of chosing the 5 numbers is by leaving out 0 or 3
when we leave out 0, the number of ways is : 2.4!
when we leave out 3, and 0 is the last digit, the number of ways is 4!
when we leave out 3 and 0 is not the last digit, the number of ways is 2.3.3!
so the sum is
4!.3+3!.6 = 3!.18= 108
pls check if i have made more goof ups :)
1is this the divisibility criteria for 6???????
dont u think that for a no. to be divisible by 6, it should be divisible by 2 and 3....
i calculated all numbers from these digits dividible by 2..... then calculated the same for 3...and took their intersection...is dis wrong????